
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),C(0,6)三点.
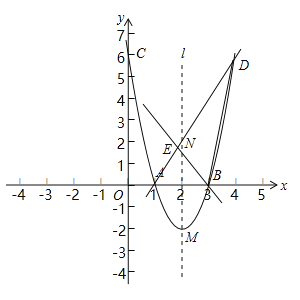
(1)求抛物线的解析式.
(2)抛物线的顶点M与对称轴l上的点N关于x轴对称,直线AN交抛物线于点D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点E的坐标.
(3)P为抛物线上的一动点,Q为对称轴上动点,抛物线上是否存在一点P,使A、D、P、Q为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=2x2﹣8x+6;(2)点E(2,2)或(3,4);(3)存在,当点P坐标为(5,16)或(﹣1,16)或(3,0)时,使A、D、P、Q为顶点的四边形为平行四边形
【解析】
(1)设抛物线解析式为:y=a(x﹣1)(x﹣3),把点C坐标代入解析式,可求解;
(2)先求出点M,点N坐标,利用待定系数法可求AD解析式,联立方程组可求点D坐标,可求S△ABD=![]() ×2×6=6,设点E(m,2m﹣2),分两种情况讨论,利用三角形面积公式可求解;
×2×6=6,设点E(m,2m﹣2),分两种情况讨论,利用三角形面积公式可求解;
(3)分两种情况讨论,利用平行四边形的性质可求解.
解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过A(1,0),B(3,0),
∴设抛物线解析式为:y=a(x﹣1)(x﹣3),
∵抛物线y=a(x﹣1)(x﹣3)(a≠0)的图象经过点C(0,6),
∴6=a(0﹣1)(0﹣3),
∴a=2,
∴抛物线解析式为:y=2(x﹣1)(x﹣3)=2x2﹣8x+6;
(2)∵y=2x2﹣8x+6=2(x﹣2)2﹣2,
∴顶点M的坐标为(2,﹣2),
∵抛物线的顶点M与对称轴l上的点N关于x轴对称,
∴点N(2,2),
设直线AN解析式为:y=kx+b,
由题意可得:![]() ,
,
解得:![]() ,
,
∴直线AN解析式为:y=2x﹣2,
联立方程组得: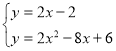 ,
,
解得: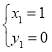 ,
,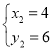 ,
,
∴点D(4,6),
∴S△ABD=![]() ×2×6=6,
×2×6=6,
设点E(m,2m﹣2),
∵直线BE将△ABD的面积分为1:2两部分,
∴S△ABE=![]() S△ABD=2或S△ABE=
S△ABD=2或S△ABE=![]() S△ABD=4,
S△ABD=4,
∴![]() ×2×(2m﹣2)=2或
×2×(2m﹣2)=2或![]() ×2×(2m﹣2)=4,
×2×(2m﹣2)=4,
∴m=2或3,
∴点E(2,2)或(3,4);
(3)若AD为平行四边形的边,
∵以A、D、P、Q为顶点的四边形为平行四边形,
∴AD=PQ,
∴xD﹣xA=xP﹣xQ或xD﹣xA=xQ﹣xP,
∴xP=4﹣1+2=5或xP=2﹣4+1=﹣1,
∴点P坐标为(5,16)或(﹣1,16);
若AD为平行四边形的对角线,
∵以A、D、P、Q为顶点的四边形为平行四边形,
∴AD与PQ互相平分,
∴![]() ,
,
∴xP=3,
∴点P坐标为(3,0),
综上所述:当点P坐标为(5,16)或(﹣1,16)或(3,0)时,使A、D、P、Q为顶点的四边形为平行四边形.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
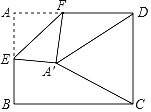
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司展销如图所示的长方形工艺品,该工艺品长60cm宽40cm,中间镶有宽度相同的三条丝绸花边.
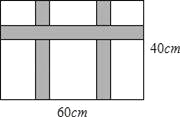
(1)若丝绸花边的面积(阴影面积)为650cm2,求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件.
(ⅰ)若想每天获利18000元,该公司应该把销售单价定为多少元?
(ⅱ)该公司应该把销售单价定为多少元,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开始时,某校九年级一班的同学为了增添教室绿色文化,打造温馨舒适的学习环境,准备到一家植物种植基地购买A、B两种花苗.据了解,购买A种花苗3盆,B种花苗5盆,则需210元;购买A种花苗4盆,B种花苗10盆,则需380元.
(1)求A、B两种花苗的单价分别是多少元?
(2)经九年级一班班委会商定,决定购买A、B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买几盆B种花苗,B种花苗每盆就降价几元,请你为九年级一班的同学预算一下,本次购买至少准备多少钱?最多准备多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的![]() 上,点D是半圆AB的中点,连接AC,BC,AD,BD,过点D作
上,点D是半圆AB的中点,连接AC,BC,AD,BD,过点D作![]() 交CB的延长线于点H.
交CB的延长线于点H.
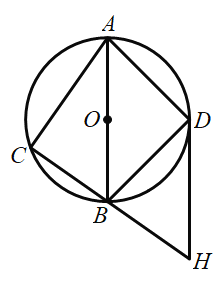
(1)求证:直线DH是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求AD,BH的长.
,求AD,BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
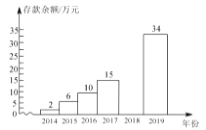
【题目】小李2014年参加工作,每年年底都把本年度收入减去支出后的余额存入银行(存款利息记入收入),2014年底到2019年底,小李的银行存款余额变化情况如下表所示:(单位:万元)
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
收入 | 3 | 8 | 9 |
| 14 | 18 |
支出 | 1 | 4 | 5 | 6 |
| 6 |
存款余额 | 2 | 6 | 10 | 15 |
| 34 |
(1)表格中![]() ________;
________;
(2)请把下面的条形统计图补充完整:(画图后标注相应的数据)
(3)请问小李在哪一年的支出最多?支出了多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100000元,公司共捐款140000元.下面是甲、乙两公司员工的一段对话:
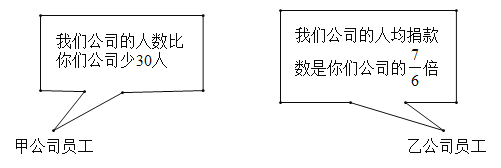
(1)甲、乙两公司各有多少人?
(2)现甲、乙两公司共同使用这笔捐款购买![]() 、
、![]() 两种防疫物资,
两种防疫物资,![]() 种防疫物资每箱15000元,
种防疫物资每箱15000元,![]() 种防疫物资每箱12000元.若购买
种防疫物资每箱12000元.若购买![]() 种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:
种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注:![]() 、
、![]() 两种防疫物资均需购买,并按整箱配送).
两种防疫物资均需购买,并按整箱配送).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售![]() ,
,![]() 两种商品,售出2件
两种商品,售出2件![]() 种商品和3件
种商品和3件![]() 种商品所得利润为700元;售出3件
种商品所得利润为700元;售出3件![]() 种商品和5件
种商品和5件![]() 种商品所得利润为1100元.
种商品所得利润为1100元.
(1)求每件![]() 种商品和每件
种商品和每件![]() 种商品售出后所得利润分别为多少元;
种商品售出后所得利润分别为多少元;
(2)由于需求量大,![]() ,
,![]() 两种商品很快售完,商场决定再一次购进
两种商品很快售完,商场决定再一次购进![]() ,
,![]() 两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么此商场至少需购进多少件
两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么此商场至少需购进多少件![]() 种商品.
种商品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com