
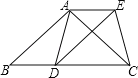
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
【答案】(1)证明见解析;(2)点D在BC的中点上时,四边形ADCE是矩形,理由见解析.
【解析】试题分析:(1)、根据平移得到AD平行且等于DE,∠B=∠EDC,根据AB=AC得出∠B=∠ACD,AC=DE,结合DC=CD得到△ACD和△ECD全等,得出AD=EC;(2)、首先得出四边形ADCE是平行四边形,结合AD⊥BC得出矩形.
试题解析:(1)、由平移可得AB∥DE,AB=DE; ∴∠B=∠EDC∵ AB=AC ∴∠B=∠ACD, AC=DE
∴∠EDC =∠ACD ∵DC=CD ∴△ACD≌△ECD(SAS) ∴AD="EC"
(2)、当点D是BC中点时,四边形ADCE是矩形
理由如下:∵AB=AC,点D是BC中点 ∴BD=DC,AD⊥BC
由平移性质可知 四边形ABDE是平行四边形 ∴AE=BD,AE∥BD ∴AE=DC,AE∥DC
∴四边形ADCE是平行四边形 ∵AD⊥BC ∴四边形ADCE是矩形


科目:初中数学 来源: 题型:
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
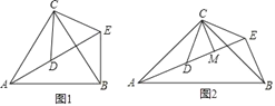
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四种说法:
(1)过直线外一点有且只有一条直线与这条直线平行;
(2)平面内,过一点能且只能作一条直线与已知直线垂直;
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短;
(4)平行于同一条直线的两条直线平行.
其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com