
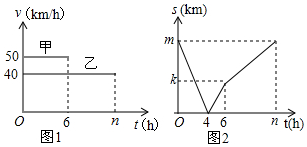
分析 (1)根据图1可以直接得到甲、乙的速度和他们的速度之和;
(2)根据题意可以得到当t=4时,两人的距离为0,此时两人相遇;
(3)根据函数图象可以得到m、n的值;
(4)根据图象中的数据可以得到k的值.
解答 解:(1)由图1可得,
甲的速度为:50km/h,乙的速度为40km/h,二人的速度之和为:50+40=90km/h,
故答案为:50,40,90;
(2)如图2所示,当t=4s时,s=0km,则表示出发4小时后二人相遇,
故答案为:相遇;
(3)由题意可得,
m=50×6+40×6=300+240=540km,n=540÷40=13.5h,
故答案为:540,13.5;
(4)由题意可得,
k=40×6=240km,
故答案为:240.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
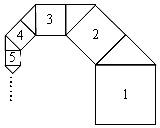 如图,第1个正方形(设边长为2)的边为第一个等腰直角三角形的斜边,第一个等腰直角三角形的直角边是第2个正方形的边,第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去.通过观察与研究,写出第2016个正方形的边长a2016为( )
如图,第1个正方形(设边长为2)的边为第一个等腰直角三角形的斜边,第一个等腰直角三角形的直角边是第2个正方形的边,第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去.通过观察与研究,写出第2016个正方形的边长a2016为( )| A. | a2016=4($\frac{1}{2}$)2015 | B. | a2016=2($\frac{\sqrt{2}}{3}$)2015 | C. | a2016=4($\frac{1}{2}$)2016 | D. | a2016=2($\frac{\sqrt{2}}{2}$)2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
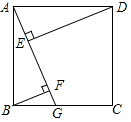 如图,G是正方形ABCD边BC上一动点(不与B、C重合).DE⊥AG于E,BF⊥AG于F,试探究线段DE、EF、BF之间满足怎样的数量关系,写出你的结论,并写出证明过程.
如图,G是正方形ABCD边BC上一动点(不与B、C重合).DE⊥AG于E,BF⊥AG于F,试探究线段DE、EF、BF之间满足怎样的数量关系,写出你的结论,并写出证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com