
|
|


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
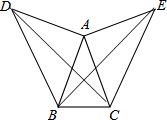 如图所示,在△ABC中,AB=AC,∠BAC=42°,F分别以AB,AC为边,作两个等腰直角△ADB和△ACE,使得∠BAD=∠CAE=90°,连接BE,CD.
如图所示,在△ABC中,AB=AC,∠BAC=42°,F分别以AB,AC为边,作两个等腰直角△ADB和△ACE,使得∠BAD=∠CAE=90°,连接BE,CD.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
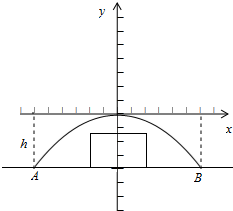 如图所示,有一抛物线形涵洞,其函数表达式为y=ax2(a≠0).涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.问该车能否通过,为什么?
如图所示,有一抛物线形涵洞,其函数表达式为y=ax2(a≠0).涵洞跨度AB=12m,内部高度h=4m.为了安全,卡车经过涵洞时,载货(矩形)最高处与其正上方顶部之间的距离不能小于0.5m.现有一辆运货卡车欲通过涵洞,经测量该车宽4m,载货最高处距地面2.5m.问该车能否通过,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
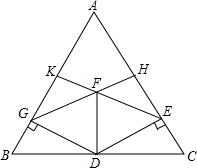 已知△ABC中,AB=AC,点D是BC中点,DE⊥AC于点E,DG⊥AB于G,EK⊥AB于K,GH⊥AC于H,EK和GH相交于F,求证:四边形DEFG是菱形.
已知△ABC中,AB=AC,点D是BC中点,DE⊥AC于点E,DG⊥AB于G,EK⊥AB于K,GH⊥AC于H,EK和GH相交于F,求证:四边形DEFG是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com