

·ÖĪö £Ø1£©ÓÉĶ¼2æÉÖŖ£¬µ±x=BE=3Ź±£¬SÓŠ×ī“óÖµ£¬“ĖŹ±£¬µćEÓėµćAÖŲŗĻ£¬¾Ż“ĖæɵĆÕż·½ŠĪABCDµÄ±ß³¤£¬ÓÉĶ¼2æÉÖŖ£¬µ±x=mŹ±£¬µćFÓėµćCÖŲŗĻ£¬“ĖŹ±£¬BF=BC=3£¬BE=tan30”ć”Į3=$\sqrt{3}$£¬¾Ż“ĖæɵĆbµÄÖµ£»
£Ø2£©·ÖĮ½ÖÖĒéæö£ŗµ±0£¼x”Ü$\sqrt{3}$Ź±£¬µćFŌŚĻ߶ĪBCÉĻ£¬“ĖŹ±£¬”÷BEFÓėÕż·½ŠĪABCDÖŲµž²æ·Ö¼“ĪŖ”÷BEF£»µ±$\sqrt{3}$£¼x”Ü3Ź±£¬µćFŌŚBCµÄŃÓ³¤ĻßÉĻ£¬“ĖŹ±£¬”÷BEFÓėÕż·½ŠĪABCDÖŲµž²æ·ÖĪŖĢŻŠĪBCGE£¬øł¾Ż”÷BEFÓėÕż·½ŠĪABCDÖŲµž²æ·ÖµÄĆ껿µÄ±ķŹ¾·½·Ø£¬æɵĆS¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£®
½ā“š  ½ā£ŗ£Ø1£©ÓÉĶ¼2æÉÖŖ£¬µ±x=BE=3Ź±£¬SÓŠ×ī“óÖµ£¬
½ā£ŗ£Ø1£©ÓÉĶ¼2æÉÖŖ£¬µ±x=BE=3Ź±£¬SÓŠ×ī“óÖµ£¬
“ĖŹ±£¬µćEÓėµćAÖŲŗĻ£¬¼“BE=BA=3£¬
”ąÕż·½ŠĪABCDµÄ±ß³¤ĪŖ3£¬
ÓÉĶ¼2æÉÖŖ£¬µ±x=mŹ±£¬µćFÓėµćCÖŲŗĻ£¬
“ĖŹ±£¬BF=BC=3£¬BE=tan30”ć”Į3=$\sqrt{3}$£¬
”ąS”÷BEF=$\frac{1}{2}$”Į$\sqrt{3}$”Į3=$\frac{3}{2}\sqrt{3}$£¬
¼“µ±m=$\sqrt{3}$Ź±£¬b=$\frac{3}{2}\sqrt{3}$£¬
¹Ź“š°øĪŖ£ŗ3£¬$\frac{3}{2}\sqrt{3}$£»
£Ø2£©ČēĶ¼1£¬µ±0£¼x”Ü$\sqrt{3}$Ź±£¬µćFŌŚĻ߶ĪBCÉĻ£¬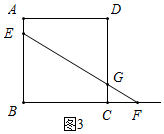
“ĖŹ±£¬”÷BEFÓėÕż·½ŠĪABCDÖŲµž²æ·Ö¼“ĪŖ”÷BEF£¬
”ßBE=x£¬”ĻEFB=30”ć£¬
”ąBF=$\sqrt{3}$x£¬
”ąS=$\frac{1}{2}$BE”ĮBF=$\frac{1}{2}$”Įx”Į$\sqrt{3}$x=$\frac{\sqrt{3}}{2}{x}^{2}$£Ø0£¼x”Ü$\sqrt{3}$£©£¬
ČēĶ¼3£¬µ±$\sqrt{3}$£¼x”Ü3Ź±£¬µćFŌŚBCµÄŃÓ³¤ĻßÉĻ£¬
“ĖŹ±£¬”÷BEFÓėÕż·½ŠĪABCDÖŲµž²æ·ÖĪŖĢŻŠĪBCGE£¬
”ßBE=x£¬”ĻEFB=30”ć£¬BC=3£¬
”ąBF=$\sqrt{3}$x£¬CF=$\sqrt{3}$x-3£¬
”ąRt”÷CFGÖŠ£¬CG=x-$\sqrt{3}$£¬
”ąS=$\frac{£ØCG+BE£©BC}{2}$=$\frac{1}{2}$£Øx-$\sqrt{3}$+x£©”Į3=3x-$\frac{3}{2}\sqrt{3}$£Ø$\sqrt{3}$£¼x”Ü3£©£¬
×ŪÉĻĖłŹö£¬S¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½ĪŖS=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2}£Ø0£¼x”Ü\sqrt{3}£©}\\{3x-\frac{3}{2}\sqrt{3}£Ø\sqrt{3}£¼x”Ü3£©}\end{array}\right.$£®
µćĘĄ “ĖĢāÖ÷ŅŖæ¼²éĮĖ¶ÆµćĪŹĢāµÄŗÆŹżĶ¼Ļó£¬Ķعżæ“Ķ¼»ńČ”ŠÅĻ¢£¬²»½öæÉŅŌ½ā¾öÉś»īÖŠµÄŹµ¼ŹĪŹĢā£¬»¹æÉŅŌĢįøß·ÖĪöĪŹĢā”¢½ā¾öĪŹĢāµÄÄÜĮ¦£®ÓĆĶ¼Ļó½ā¾öĪŹĢāŹ±£¬¹Ų¼üŹĒŅŖĄķĒåĶ¼ĻóµÄŗ¬Ņ弓»įŹ¶Ķ¼£®


 ĆūŹ¦Öøµ¼ĘŚÄ©³å“Ģ¾ķĻµĮŠ“š°ø
ĆūŹ¦Öøµ¼ĘŚÄ©³å“Ģ¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2016-2017ѧğ¹ć¶«Ź”½ŅŃōŹŠĘßÄź¼¶ĻĀѧʌµŚŅ»“ĪŌĀæ¼ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
ĻČ»Æ¼ņ£¬ŌŁĒóÖµ£ŗ [(2x£«y)2£(2x£y) (2x£«y)]”Ā(2y)£¬ĘäÖŠx£½2, y=£1.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2017½ģ¹ćĪ÷ĀķɽĻŲĆń×å֊ѧ“ŗ¼¾Ń§ĘŚµŚŅ»“ĪŌĀæ¼°ĖÄź¼¶ŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗµ„Ń”Ģā
Ę½ĆęÖ±½Ē×ų±źĻµÉĻµćA”¢BµÄ×ų±ź·Ö±šĪŖ(4,0)”¢(0,3),ŌņĻ߶ĪAB³¤ĪŖ( )
A. 6 B. 5 C. 4 D. 3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
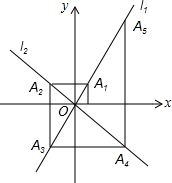 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŗÆŹży=2xŗĶy=-xµÄĶ¼Ļó·Ö±šĪŖÖ±Ļßl1£¬l2£¬¹żµć£Ø1£¬0£©×÷xÖįµÄ“¹Ļß½»l1ÓŚµćA1£¬¹żµćA1×÷yÖįµÄ“¹Ļß½»l2ÓŚµćA2£¬¹żµćA2×÷xÖįµÄ“¹Ļß½»l2ÓŚµćA3£¬¹żµćA3×÷yÖįµÄ“¹Ļß½»l2ÓŚµćA4£¬”ŅĄ“Ī½ųŠŠĻĀČ„£¬ŌņµćA2007µÄ×ų±źĪŖ£Ø21008£¬21009£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŗÆŹży=2xŗĶy=-xµÄĶ¼Ļó·Ö±šĪŖÖ±Ļßl1£¬l2£¬¹żµć£Ø1£¬0£©×÷xÖįµÄ“¹Ļß½»l1ÓŚµćA1£¬¹żµćA1×÷yÖįµÄ“¹Ļß½»l2ÓŚµćA2£¬¹żµćA2×÷xÖįµÄ“¹Ļß½»l2ÓŚµćA3£¬¹żµćA3×÷yÖįµÄ“¹Ļß½»l2ÓŚµćA4£¬”ŅĄ“Ī½ųŠŠĻĀČ„£¬ŌņµćA2007µÄ×ų±źĪŖ£Ø21008£¬21009£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| x | m | 0 | 2 |
| y1 | 4 | 3 | t |
| y2 | 6 | n | -1 |
| A£® | -$\frac{1}{3}$ | B£® | -3 | C£® | $\frac{1}{2}$ | D£® | 5 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ĮāŠĪABCDµÄ±ßABĪŖ5£¬¶Ō½ĒĻßACĪŖ8£¬ŌņĮāŠĪABCDµÄĆ껿ĪŖ24£®
ĮāŠĪABCDµÄ±ßABĪŖ5£¬¶Ō½ĒĻßACĪŖ8£¬ŌņĮāŠĪABCDµÄĆ껿ĪŖ24£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
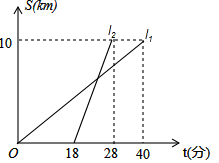 ¼×”¢ŅŅĮ½ČĖŅŌĻąĶ¬Ā·ĻßĒ°Ķł¾ąĄėµ„Ī»10kmµÄÅąŃµÖŠŠÄ²Ī¼ÓѧĻ°£¬Ķ¼l1£¬l2·Ö±š±ķŹ¾¼×”¢ŅŅĮ½ČĖĒ°ĶłÄæµÄµŲĖł×ßµÄĀ·³ĢS£ØĒ§Ć×£©Ėꏱ¼ät£Ø·Ö£©±ä»ÆµÄŗÆŹżĶ¼Ļó£¬ŅŌĻĀĖµ·Ø¢Ł¼×±ČŅŅĢįĒ°12·ÖÖÓµ½“ļ£»¢Ś¼×µÄĘ½¾łĖŁ¶ČĪŖ15Ē§Ć×/Š”Ź±£»¢Ū¼×ŅŅĻąÓöŹ±£¬ŅŅ×ßĮĖ6Ē§Ć×£»¢ÜŅŅ³ö·¢6·ÖÖÓŗó×·ÉĻ¼×£¬ĘäÖŠÕżČ·µÄÓŠ£Ø””””£©
¼×”¢ŅŅĮ½ČĖŅŌĻąĶ¬Ā·ĻßĒ°Ķł¾ąĄėµ„Ī»10kmµÄÅąŃµÖŠŠÄ²Ī¼ÓѧĻ°£¬Ķ¼l1£¬l2·Ö±š±ķŹ¾¼×”¢ŅŅĮ½ČĖĒ°ĶłÄæµÄµŲĖł×ßµÄĀ·³ĢS£ØĒ§Ć×£©Ėꏱ¼ät£Ø·Ö£©±ä»ÆµÄŗÆŹżĶ¼Ļó£¬ŅŌĻĀĖµ·Ø¢Ł¼×±ČŅŅĢįĒ°12·ÖÖÓµ½“ļ£»¢Ś¼×µÄĘ½¾łĖŁ¶ČĪŖ15Ē§Ć×/Š”Ź±£»¢Ū¼×ŅŅĻąÓöŹ±£¬ŅŅ×ßĮĖ6Ē§Ć×£»¢ÜŅŅ³ö·¢6·ÖÖÓŗó×·ÉĻ¼×£¬ĘäÖŠÕżČ·µÄÓŠ£Ø””””£©| A£® | 4øö | B£® | 3øö | C£® | 2øö | D£® | 1øö |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com