
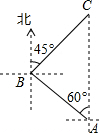
 科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.
科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离. 分析 过B作BD⊥AC于点D,在直角△ABD中利用三角函数求得BD的长,然后在直角△BCD中利用三角函数求得BC的长.
解答 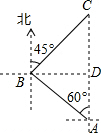 解:过B作BD⊥AC于点D.
解:过B作BD⊥AC于点D.
在Rt△ABD中,AD=AB•cos∠BAD=4cos60°=4×$\frac{1}{2}$=2(千米),
BD=AB•sin∠BAD=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$(千米),
∵△BCD中,∠CBD=45°,
∴△BCD是等腰直角三角形,
∴CD=BD=2$\sqrt{3}$(千米),
∴BC=$\sqrt{2}$BD=2$\sqrt{6}$(千米).
答:B,C两地的距离是2$\sqrt{6}$千米.
点评 此题考查了方向角问题.此题难度适中,解此题的关键是将方向角问题转化为解直角三角形的知识,利用三角函数的知识求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 零上3℃ | B. | 零下3℃ | C. | 零上7℃ | D. | 零下7℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com