
| A. | 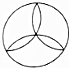 | B. |  | C. | 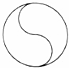 | D. | 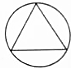 |
科目:初中数学 来源: 题型:选择题
 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )| A. | 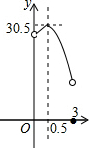 | B. | 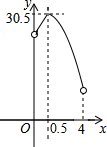 | C. |  | D. | 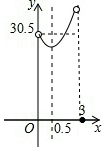 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
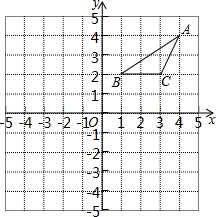 如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )| A. | A′(4,-4) | B. | B′(-1,2) | C. | A″(-4,-4) | D. | C″(-2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.
如图,在平面直角坐标系xOy中,一次函数y=-ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-4,-2),B(m,4),与y轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.
如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和小颖家住在同一地铁站口的同一小区内.星期天两人各自去南禅寺书城买书.小颖乘地铁,小明由爸爸开私家车前往.已知该段私家车行驶的路线和地铁路线恰好在同一直线上,且私家车的速度比地铁慢.他们早上同时出发,设出发后的时间为t分钟,小明和小颖之间的距离为S,S与t的部分函数图象如图所示.
小明和小颖家住在同一地铁站口的同一小区内.星期天两人各自去南禅寺书城买书.小颖乘地铁,小明由爸爸开私家车前往.已知该段私家车行驶的路线和地铁路线恰好在同一直线上,且私家车的速度比地铁慢.他们早上同时出发,设出发后的时间为t分钟,小明和小颖之间的距离为S,S与t的部分函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
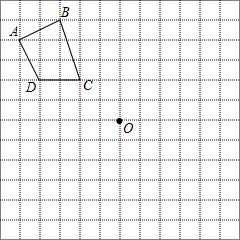 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和格点O.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点)和格点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com