
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
【答案】B
【解析】
根据“抛物线![]() 与直线
与直线![]() 有两个不同的交点”即可判断①③;根据抛物线的对称轴为直线x=1即可判断②;根据等腰直角三角形的性质,用c表达出两个交点,代入抛物线解析式计算即可判断④.
有两个不同的交点”即可判断①③;根据抛物线的对称轴为直线x=1即可判断②;根据等腰直角三角形的性质,用c表达出两个交点,代入抛物线解析式计算即可判断④.
解:∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,
有两个不同的交点,
∴![]() 有两个不相等的实数根,即
有两个不相等的实数根,即![]() 有两个不相等的实数根,故③正确,
有两个不相等的实数根,故③正确,
∴![]() ,解得:
,解得:![]() ,故①正确;
,故①正确;
∵抛物线的对称轴为直线x=1,且抛物线开口向上,
∴当x=1时,![]() 为最小值,故②正确;
为最小值,故②正确;
若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,
则顶点(1,c-2)到直线y=2的距离等于两交点距离的一半,
∵顶点(1,c-2)到直线y=2的距离为2-(c-2)=4-c,
∴两交点的横坐标分别为1-(4-c)=c-3与1+(4-c)=5-c
∴两交点坐标为(c-3,2)与(5-c,2),
将(c-3,2)代入![]() 中得:
中得:![]()
解得:![]() 或
或![]()
∵![]() ,
,
∴![]() ,故④错误,
,故④错误,
∴正确的有①②③,
故选:B.


科目:初中数学 来源: 题型:
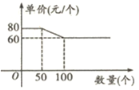
【题目】某批发部某一玩具价格如图所示,现有甲、乙两个商店,计划在“六一”儿童节前到该批发部购买此类玩具,两商店所需玩具总数为120个,乙商店所需数量不超过50个,设甲商店购买![]() 个,如果甲、乙两商店分别购买玩具,两商店需付款总和为
个,如果甲、乙两商店分别购买玩具,两商店需付款总和为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若甲商店购买不超过100个,请说明甲、乙两商店联合购买比分别购买最多可节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10![]() km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4![]() km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.

A.8![]() B.9
B.9![]() C.6
C.6![]() D.7
D.7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
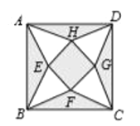
【题目】将一个边长为4的正方形![]() 分割成如图所示的9部分,其中
分割成如图所示的9部分,其中![]() ,
,![]() ,
,![]() ,
,![]() 全等,
全等,![]() ,
,![]() ,
,![]() ,
,![]() 也全等,中间小正方形
也全等,中间小正方形![]() 的面积与
的面积与![]() 面积相等,且
面积相等,且![]() 是以
是以![]() 为底的等腰三角形,则
为底的等腰三角形,则![]() 的面积为( )
的面积为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
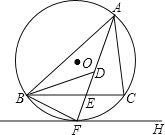
【题目】如图,![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,连结
,连结![]() .下列结论:①
.下列结论:①![]() 平分
平分![]() ;②连接
;②连接![]() ,点
,点![]() 为
为![]() 的外心;③
的外心;③![]() ;④若点
;④若点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是
的最小值是![]() .其中一定正确的是__________(把你认为正确结论的序号都填上).
.其中一定正确的是__________(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,如表是
的函数,如表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.
之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:

(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①![]() 对应的函数值
对应的函数值![]() 约为 ;
约为 ;
②该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
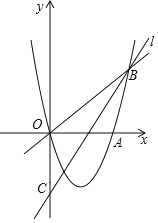
【题目】如图,抛物线y=ax2+bx+c经过O、A(4,0)、B(5,5)三点,直线l交抛物线于点B,交y轴于点C(0,﹣4).点P是抛物线上一个动点.
(1)求抛物线的解析式;
(2)点P关于直线OB的对称点恰好落在直线l上,求点P的坐标;
(3)M是线段OB上的一个动点,过点M作直线MN⊥x轴,交抛物线于点N.当以M、N、B为顶点的三角形与△OBC相似时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
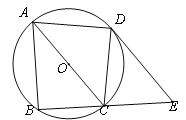
【题目】如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为![]() 的中点,过点D作DE∥AC,交BC的延长线于点E.
的中点,过点D作DE∥AC,交BC的延长线于点E.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若CE=![]() ,AB=6,求⊙O的半径.
,AB=6,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com