
【题目】如图1所示,在△ABC中,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,连接AM、AN.
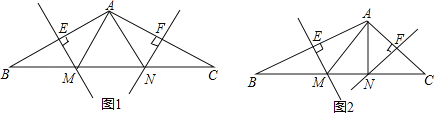
(1)求证:△AMN的周长=BC;
(2)若AB=AC,∠BAC=120°,试判断△AMN的形状,并证明你的结论;
(3)若∠C=45°,AC=3![]() ,BC=9,如图2所示,求MN的长.
,BC=9,如图2所示,求MN的长.
【答案】(1)见解析;(2)△AMN是等边三角形,见解析;(3)![]()
【解析】
(1)根据线段垂直平分线的性质得到EA=EB,NA=CA,根据三角形的周长公式证明结论;
(2)根据等腰三角形的性质、三角形内角和定理得到∠B=∠C=30°,根据三角形的外角性质、等边三角形的判定定理证明;
(3)证明ANM=90°,根据勾股定理求出AN、NC,根据勾股定理列式计算得到答案.
(1)证明:∵EM是AB的垂直平分线,
∴EA=EB,
同理,NA=CA,
∴△AMN的周长=MA+MN+NA=MB+MN+NC=BC;
(2)解:△AMN是等边三角形,
理由如下:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EA=EB,
∴∠MAB=∠B=30°,
∴∠AMN=∠MAB+∠B=60°,
同理可得,∠ANM=60°,
∴△AMN是等边三角形;
(3)解:∵NC=NA,
∴∠NAC=∠C=45°,
∴∠ANM=∠ANC=90°,
设NC=NA=x,
由勾股定理得,NA2+NC2=AC2,即x2+x2=(3![]() )2,
)2,
解得,x=3,即NC=NA,
∴MB=MA=6﹣MN,
在Rt△AMN中,NA2+MN2=AM2,即32+MN2=(6﹣MN)2,
解得,MN=![]() .
.


科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子1张或椅子4把,现计划用120块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
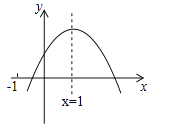
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
①2a+b=0;
②当﹣1≤x≤3时,y<0;
③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )

A. ①②④ B. ①②③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①abc>0,
②a﹣b+c<0,
③2a=b,
④4a+2b+c>0,
⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .
.
其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
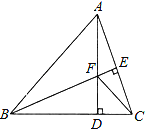
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数![]() 的图象上.那么k的值是
的图象上.那么k的值是
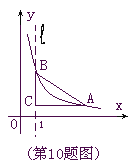
A .3 B.6 C.12 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 、
、![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万元购买
种型号电脑的数量与用8万元购买![]() 种型号电脑的数量相同.求
种型号电脑的数量相同.求![]() 、
、![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com