
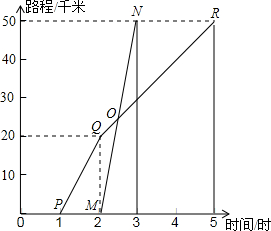
 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.分析 (1)时间应看横轴,在前面的就是早出发的.
(2)路程应看y轴.
(3)相遇时间看甲和乙的函数图象交点处的时间即可.
解答 解:(1)甲比乙出发更早,要早2-1=1小时;
(2)乙比甲早到B城,早了5-3=2个小时;
(3)由图可知:M(2,0),N(3,50),Q(2,20),R(5,50)
设直线QR的函数表达式为y1=k1x+b1,直线MN的函数表达式为y2=k2x+b2,
将各点坐标代入对应的表达式,得:$\left\{\begin{array}{l}{20=2{k}_{1}+{b}_{1}}\\{50=5{k}_{1}+{b}_{1}}\end{array}\right.$,$\left\{\begin{array}{l}{0=2{k}_{2}+{b}_{2}}\\{50=3{k}_{2}+{b}_{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{{k}_{1}=10}\\{{b}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{k}_{2}=50}\\{{b}_{2}=-100}\end{array}\right.$.
∴y1=10x,y2=50x-100,
联立两式可得直线QR、MN的交点的坐标为O(2.5,25),
2.5-2=0.5,
所以乙出发半小时后追上甲.
点评 本题考查了一次函数的应用,主要利用了追及问题的等量关系,准确识图并根据函数图象的变化情况获取信息是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
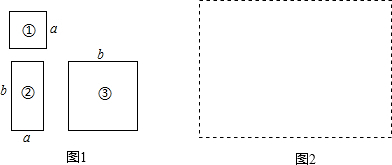
 已知:如图,△CBE是一个锐角三角形,分别以CB,CE为边向外侧作等边三角形ABC和等边三角形CDE,连接AE、BD.
已知:如图,△CBE是一个锐角三角形,分别以CB,CE为边向外侧作等边三角形ABC和等边三角形CDE,连接AE、BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,-3 | B. | -1,-6 | C. | 1,-6 | D. | 1,6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
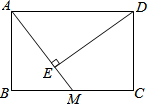 如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )
如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为( )| A. | 2 | B. | $\frac{12}{5}$ | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
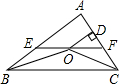 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±5 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ±$\sqrt{49}$=±7 | D. | $\sqrt{-100}$=10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com