练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，五边形ABCDE中，AB=AE，BC=DE，∠ABC=∠AED，点F是CD的中点．
    求证：AF⊥CD．
    分析：连接AC，AD，可证明△ABC≌△AED，进而得到AC=AD，再利用等腰三角形的性质：三线合一即可得到AF⊥CD．
    解答：证明：连接AC，AD，
    在△ABC和△AED中，
    AB=AE
    ∠ABC=∠AED
    BC=DE
    ，
    ∴△ABC≌△AED（SAS），
    ∴AC=AD，
    ∵点F是CD的中点，
    ∴AF⊥CD．
    点评：本题考查了全等三角形的判定和性质以及等腰三角形的判定和性质，解题的关键是连接AC，AD构造全等三角形．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•钦州）如图所示，把一张矩形纸片对折，折痕为AB，在把以AB的中点O为顶点的平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

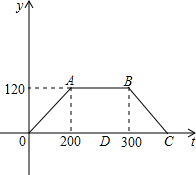    小明参加汽车驾驶培训，在实际操作考试时，被要求进行启动加速、匀速运行、制动减速三个连贯过程，在加速和减速运动过程中，路程和速度均满足关系s=v0t+
    12
    at2    ，v0为加速或减速的起始速度，加速时a为正，减速时a为负，匀速时a=0，加速或减速t秒后的瞬时速度v=v0+at，小明在操作中瞬时速度v与时间t的关系如图所示，其中OA为匀加速，AB为匀速，BC为匀减速．
    （1）若减速过程与加速过程完全相反，即BC与OA关于AB的中垂线成轴对称，求BC的解析式．
    （2）当0≤t≤300时，求汽车行驶的路程s与时间t的函数关系式．
    （3）汽车行驶t秒后，
    ①若经途中D点，过点D作垂线交AB于点E，试证明汽车行驶的路程恰等于四边形OAED的面积．
    ②若汽车行驶至M点，过点M做垂线交BC于点N，汽车行驶的路程是否等于五边形OABNM的面积呢？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源：新课标读想练　七年级数学(下) 人教版 题型：047

    如图所示，五边形ABCDE中，AB＝AE，BC＝ED，∠B＝∠E．求证：∠C＝∠D．

    查看答案和解析>>

    科目：初中数学 来源：课堂三级讲练数学九年级(上) 题型：022

    如图所示，五边形ABCDE是五五边形，曲线EFGHIJ……叫做“正五边形ABCDE的渐开线”，其中，，，，…的圆心依次接A、B、C、D、E循环，它们依次相连接，如果AB＝1，那么曲线EFGHIJ的长度为________(结果保留π)．

    查看答案和解析>>

    同步练习册答案