
����Ŀ����ƽ��ֱ������ϵ�У���֪A��B��������y=ax2��a��0����������ͬ�ĵ㣬����A�ڵڶ����ޣ�B�ڵ�һ���ޣ�
��1����ͼ1��ʾ����ֱ��AB��x��ƽ�У���AOB=90�㣬��AB=2ʱ����������ߵĽ���ʽ��A��B����ĺ�����ij˻���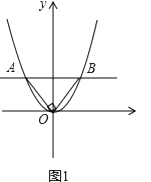
��2����ͼ2��ʾ���ڣ�1������õ��������ϣ���ֱ��AB��x�ƽ�У���AOB��Ϊ90��ʱ����֤��A��B���������ij˻���һ����ֵ��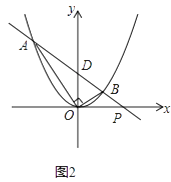
��3���ڣ�2���������£����ֱ��AB��x�ᡢy��ֱ��ڵ�P��D���ҵ�B�ĺ�����Ϊ ![]() ����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��ͼ1��
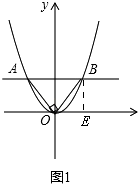
��BE��x�ᣬ
���AOB�ǵ���ֱ�������Σ�
��BE=OE= ![]() AB=1��
AB=1��
��A����1��1����B��1��1����
��A��B����ĺ�����ij˻�Ϊ��1��1=��1��
��������y=ax2��a��0����A��B��
��a=1��
��������y=x2��
��2���⣺��ͼ2��
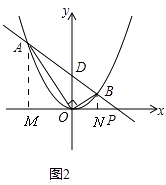
��BN��x�ᣬ��AM��x�ᣬ
���AOB=AMO=��BNO=90�㣬
���MAO=��BON��
���AMO�ס�ONB��
�� ![]() ��
��
��AM��BN=OM��ON��
��A��x1��y1����B��x2��y2�����������ϣ�
��AM=y1=x12��BN=y2=x22��OM=��x1��ON=x2��
��x12��x22=��x1��x2��
��x1��x2=��1��
��A��B���������ij˻���һ����ֵ��
��3���⣺�ɣ�2���ã�A��B���������ij˻���һ����ֵΪ��1��
�ߵ�B�ĺ�����Ϊ ![]() ��
��
���A�ĺ�����Ϊ��2��
��A��B���������ϣ�
��A����2��4����B�� ![]() ��
�� ![]() ����
����
��ֱ��AB����ʽΪy=�� ![]() x+1��
x+1��
��P�� ![]() ��0����D��0��1��
��0����D��0��1��
��Q��n��0����
��DP2= ![]() ��PQ2=��n��
��PQ2=��n�� ![]() ��2��DQ2=n2+1
��2��DQ2=n2+1
�ߡ�QDPΪ���������Σ�
���DP=PQ��
��DP2=PQ2��
�� ![]() =��n��
=��n�� ![]() ��2��
��2��
��n= ![]() ��
��
��Q1�� ![]() ��0����Q2��
��0����Q2�� ![]() ��0��
��0��
��DP=DQ��
��DP2=DQ2��
�� ![]() =n2+1��
=n2+1��
��n= ![]() ���ᣩ��n=��
���ᣩ��n=�� ![]() ��
��
Q3���� ![]() ��0��
��0��
��PQ=DQ��
��PQ2=DQ2��
�ࣨn�� ![]() ��2=n2+1
��2=n2+1
��n=�� ![]() ��
��
��Q4���� ![]() ��0����
��0����
����ڵ�Q����ΪQ1�� ![]() ��0����Q2��
��0����Q2�� ![]() ��0����Q3����
��0����Q3���� ![]() ��0����Q4����
��0����Q4���� ![]() ��0����
��0����
����������1���������������ʼ�����ϵ�������������ʽ��������˻�����2��ͨ������BN��x�ᣬ��AM��x�ᡱ�������������Σ�����AMO�ס�ONB����Ӧ�߳ɱ�����ת��Ϊ�˻�ʽ��A��B���������ij˻���һ����ֵ����3�����ã�2���Ľ������A��B���꣬����QDPΪ���������Σ���������ۣ�����DP=PQ��DP=DQ��PQ=DQ���ֱ����Q����.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F��ƽ���ı���ABCD�ĶԽ���AC�ϵ� ���㣬AE=CF��

��֤����1����ADF�ա�CBE
��2��EB��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ӳ��У�![]() �㣩����������
�㣩����������![]() ����С��ң�
����С��ң�![]() �㣩����������
�㣩����������![]() ����С�żң�
����С�żң�![]() �㣩��Ȼ���ֻ�ͷ������
�㣩��Ȼ���ֻ�ͷ������![]() ����С�¼ң�
����С�¼ң�![]() �㣩�����ص����У�
�㣩�����ص����У�
��1���Գ���Ϊԭ�㣬����Ϊ��������![]() ��ʾ
��ʾ![]() ���������ᣬ���ڸ������ϱ�ʾ
���������ᣬ���ڸ������ϱ�ʾ![]() ��
��![]() ��
��![]() ��
��![]() ��λ�ã�
��λ�ã�
��2��С�¼ң�![]() �㣩��С��ң�
�㣩��С��ң�![]() �㣩�ж�Զ��
�㣩�ж�Զ��
��3��������շѱ����£�![]() ���ڰ���
���ڰ���![]() �շ�
�շ�![]() Ԫ������
Ԫ������![]() ���ְ�ÿǧ��
���ְ�ÿǧ��![]() Ԫ�շѣ���ӳ��г������ص�����һ�����Ѷ���Ԫ��
Ԫ�շѣ���ӳ��г������ص�����һ�����Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̨����һ����Ȼ�ֺ�������̨������ΪԲ�ģ�����Χ��ʮǧ��Χ���������籩���м�ǿ���ƻ�������ʱij̨�������ں���B�������غ�����A�����Ϸ���240ǧ�ף������ķ���Ϊ12����ÿԶ��̨������25ǧ�ף�̨��ͻ����һ������ͼ��ʾ����̨����������20ǧ��/ʱ���ٶ��ر�ƫ��30��������C�ƶ�����̨�����ĵķ������䣬���������ܷ����ﵽ��4���������̨��Ӱ�죮 ���ʣ�

��1��A�����Ƿ���ܵ�̨��Ӱ�죿��˵�����ɣ�
��2�������ܵ�̨��Ӱ�죬��ǫ̂��Ӱ��ó��еij���ʱ���ж��
��3���ó����ܵ�̨��Ӱ���������Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������ס������ֻ��ܣ����������ֻ���20�裬���ֻ���50�裬��Ҫ900Ԫ�����������ֻ���40�裬���ֻ���30�裬��Ҫ960Ԫ��
��1�����ס������ֻ���ÿ��������Ԫ��
��2���û��깺���ף������ֻ��ܹ�100�裬���ֻ���ÿ���ۼ�20Ԫ�����ֻ���ÿ���ۼ�16Ԫ���ָû����100�軨��ȫ���۳�������������480Ԫ�������ٹ������ֻ��ܶ����裿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ���ʾ���й����˵�������غϵ���������ɵĽ���0�㣩��
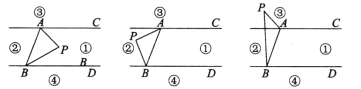
��1��������P���ڵڢٲ���ʱ����֤����APB����PAC����PBD��
��2��������P���ڵڢڲ���ʱ����APB����PAC����PBD�Ƿ������ֱ�ӻش������������
��3��������P�ڵڢ۲���ʱ��ȫ��̽����PAC����APB����PBD֮��Ĺ�ϵ����д������P�ľ���λ�ú���Ӧ�Ľ��ۣ�ѡ������һ�ֽ��ۼ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�����BD��
��1����ͼ1��AE��BD��E��ֱ��д����BAE�Ķ�����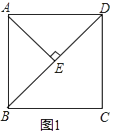
��2����ͼ1���ڣ�1���������£�����AEB��A��ת���ģ�����ʱ�뷽����ת30���õ���AB��E�䣬AB����BD����M��AE����ӳ�����BD����N��
�������ⲹȫͼ1��
���õ�ʽ��ʾ�߶�BM��DN��MN֮���������ϵ����֤����
��3����ͼ2��E��F�DZ�BC��CD�ϵĵ㣬��CEF�ܳ���������ABCD�ܳ���һ�룬AE��AF�ֱ���BD����M��N��д���ж��߶�BM��DN��MN֮��������ϵ��˼·��������д�������������̣�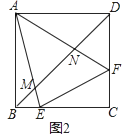
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
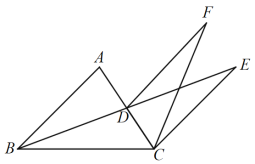
����Ŀ����ͼ�٣�����ABC�У���ABC���ACB��ƽ�����ཻ�ڵ�P��
��1�������A=80��������BPC�Ķ�����
��2����ͼ�ڣ�����ABC�����MBC����NCB�Ľ�ƽ���߽��ڵ�Q����̽����Q����A֮���������ϵ��
��3����ͼ�ۣ��ӳ��߶�BP��QC���ڵ�E����BQE�У�����һ���ڽǵ�����һ���ڽǵ�2��������A�Ķ���.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() ���ϵ����ߣ�����
���ϵ����ߣ�����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() ����֤��
����֤��
��1��![]() ��
��
��2��CAƽ��![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com