
分析 在△ABC中构建一截线,满足把△ABC分成两个等腰三角形,分四种情况画图讨论:分别过顶点C和B,如图所示,分别求出∠C的度数.
解答 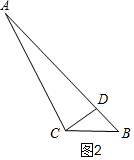
 解:如图1,刀痕为BD时,
解:如图1,刀痕为BD时,
则CD=BC,AD=BD,
∴∠ABD=∠A=16°,∠CDB=∠CBD=32°
∴∠C=180°-32°-32°=116°
如图2,刀痕为CD时,
则AC=AD,CD=BD,
∴∠ACD=∠ADC=$\frac{180°-16°}{2}$=82°
∵∠B=∠BCD,∠ADC=∠B+∠BCD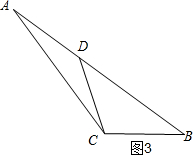
∴∠B=∠BCD=41°
∴∠ACB=∠ACD+∠BCD=82°+41°=123°
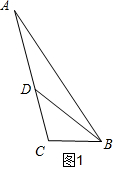
如图3,刀痕为BD时,
则CD=BC,AD=CD,
∴∠ACD=∠A=16°,∠CDB=∠CBD=32°,
∴∠BCD=180°-32°-32°=116°,
∴∠ACB=∠ACD+∠BCD=11°+16°=132°,
如图4,刀痕为CD时,
则CD=BD,AD=CD,
∴∠ACD=∠A=16°,∠CDB=32°,∠DCB=$\frac{180°-32°}{2}$=74°,
∴∠ACB=∠ACD+∠BCD=16°+74°=90°,
综上所述,则∠C的度数:90°或123°或116°或132°.
故答案为:90°或123°或116°或132°.
点评 本题考查了等腰三角形的性质和三角形的外角定理,熟练掌握等边对等角,等角对等边是本题的关键;明确三角形的一个外角等于与它不相邻的两个内角的和.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
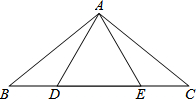 如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,请你添加一个条件使∠DAB=∠EAC.
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,请你添加一个条件使∠DAB=∠EAC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
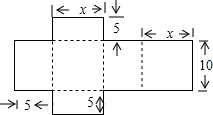 如图,已知某长方体的展开图的面积为310cm2,根据图中数据可列出关于x的一元一次方程为2×(10x+5x+5×10)=310,x的值为7.
如图,已知某长方体的展开图的面积为310cm2,根据图中数据可列出关于x的一元一次方程为2×(10x+5x+5×10)=310,x的值为7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com