
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
 为了了解某校七年级学生完成数学课前预习的惰况,随机抽取该年级100名学生进行了调查,调查结果分为四类:
为了了解某校七年级学生完成数学课前预习的惰况,随机抽取该年级100名学生进行了调查,调查结果分为四类:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现在的乐陵已经实现村村通公路,现有两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
现在的乐陵已经实现村村通公路,现有两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4),矩形ABCD的顶点A与点O重合,点B、D的坐标分别为(0,3)、(-2,0),将矩形ABCD以每秒1个单位长度的速度沿x轴的正方向平移,同时点P也以每秒a个单位长度从A出发,沿A→B→C→D运动,到点D停止,设矩形移动的时间为t(s).
如图,在平面直角坐标系中,抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4),矩形ABCD的顶点A与点O重合,点B、D的坐标分别为(0,3)、(-2,0),将矩形ABCD以每秒1个单位长度的速度沿x轴的正方向平移,同时点P也以每秒a个单位长度从A出发,沿A→B→C→D运动,到点D停止,设矩形移动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
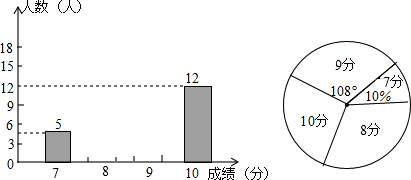
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com