

分析 (1)猜想:四边形CGFH是菱形.只要证明△FOG≌△COH,推出四边形FHCG是平行四边形即可解决问题;
(2)如图2中,延长EF交CD的延长线于M.只要证明四边形CGFH是正方形,以及△AFE≌△DFM即可解决问题;
解答 解:(1)猜想:四边形CGFH是菱形.
理由:如图1中,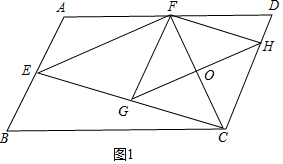
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AEC+∠ECD=180°,
∵∠FEC=$\frac{1}{2}$∠AEC,∠FCE=$\frac{1}{2}$∠DCE,
∴∠FEC+∠FCE=90°,
∴∠EFC=90°,
∵GH∥EF,
∴∠GOC=∠EFC=90°,
∵CG=EG,GO∥EF,
∴OF=OC,
在Rt△EFC中,∵EG=GC,
∴FG=GC,
∴∠GCF=∠GFC=∠FCD,
∵∠FOG=∠COH,
∴△FOG≌△COH,
∴OG=OH,
∵OF=OC,
∴四边形FGCH是平行四边形,
∵GF=GC,
∴四边形CGFH是菱形.
(2)如图2中,延长EF交CD的延长线于M.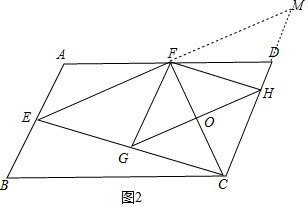
∵EF=CF,∠EFC=90°,EG=CG,
∴FG⊥EC,
∴∠FGC=90°,
∴四边形CGFH是正方形,
∴∠FCG=∠FCH=45°,
∴EF=FM,
∵∠AFE=∠MFD,∠AEF=∠M,
∴△AFE≌△DFM,
∴AE=DM=2,AF=DF,
∴CM=CD+DM=6,
∵FH⊥CM,CF=FM,
∴CH=HM=FH=3,
在Rt△DFH中,DF=$\sqrt{F{H}^{2}+D{H}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴AD=2DF=2$\sqrt{10}$.
点评 本题考查平行四边形的性质、菱形的判定、正方形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
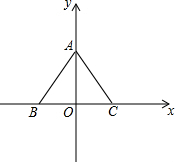 如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.
如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=x2=0 | B. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
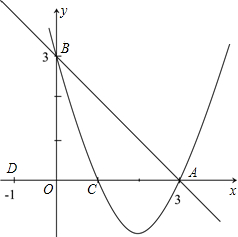 如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.
如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com