
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600(50-x) |
分析 (1)根据题意可以将表格中的数据补充完整,并求出y与x的函数关系式;
(2)根据(1)中的答案和题意可以列出相应的不等式,从而可以解答本题.
解答 (1)由题意可得,
当x=7时,50-x=43,
当x=3时,粗加工获利为:(4000-600-3000)×3=1200,精加工获利为:(4500-3000-900)×47=28200,
故答案为:43、50-x;1200、28200,400x、600(50-x);
y与x的函数关系式是:y=400x+600(50-x)=-200x+30000,
即y与x的函数关系式是y=-200x+30000;
(2)设应把x吨进行粗加工,其余进行精加工,由题意可得
$\frac{1}{3}x+\frac{1}{2}(50-x)≤20$,
解得,x≥30,
∵y=-200x+30000,
∴当x=30时,y取得最大值,此时y=24000,
即应把30吨进行粗加工,另外20吨进行精加工,这样才能获得最大利润,最大利润为24000元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的性质解答问题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
 已知y=-$\frac{1}{2}$x2+2x+6
已知y=-$\frac{1}{2}$x2+2x+6| x | … | -2 | 0 | 2 | 4 | 6 | … |
| y | … | 0 | 6 | 8 | 6 | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
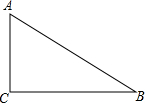 如图,在△ABC中,∠C=90°,∠B=37°,若BC=3.求:AC、AB的长(结果保留小数点后一位).参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.
如图,在△ABC中,∠C=90°,∠B=37°,若BC=3.求:AC、AB的长(结果保留小数点后一位).参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com