
【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为![]() ,求EF的长.
,求EF的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由正方形的性质得出AD=AB,证出∠DAF=∠ABE,由AAS证明△ADF≌△BAE,得出AF=BE,DF=AE,即可得出结论;
(2)设DF=a,AF=b,EF=DF-AF=a-b>0,由已知条件得出DF+AF=![]() ,即a+b=
,即a+b=![]() ,由勾股定理得出a2+b2=1,再由完全平方公式得出a-b即可.
,由勾股定理得出a2+b2=1,再由完全平方公式得出a-b即可.
(1)证明:∵BE⊥AP,DF⊥AP,
∴∠DFA=∠AEB=90°,∠ABE+∠BAE=90°,
∵四边形ABCD为正方形,∴AD=AB,∠DAB=90°=∠DAF+∠BAE,
∴∠DAF=∠ABE,
在△ADF和△BAE中,∠DAF=∠ABE,∠DFA=∠AEB,AD=AB,
∴△ADF≌△BAE(AAS),
∴AF=BE,DF=AE,
∴EF=AE﹣AF=DF﹣BE;
(2)解:设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,∵△ADF的周长为![]() ,AD=1,∴DF+AF=
,AD=1,∴DF+AF=![]() ,
,
即a+b=![]() ,由勾股定理得:DF2+AF2=AD2,即a2+b2=1,
,由勾股定理得:DF2+AF2=AD2,即a2+b2=1,
∴(a﹣b)2=2(a2+b2)﹣(a+b)2=2﹣![]() ,∴a﹣b=
,∴a﹣b=![]() ,即EF=
,即EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为﹣1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
(1)用含有t的代数式表示AM的长为
(2)当t= 秒时,AM+BN=11.
(3)若点A、B与线段MN同时移动,点A以每秒2个单位速度向数轴的正方向移动,点B以每秒1个单位的速度向数轴的负方向移动,在移动过程,AM和BN可能相等吗?若相等,请求出t的值,若不相等,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元。现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售。某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).
(1)用代数式表示(所填式子需化简):
当购买乒乓球的盒数为x盒时,在甲店购买需付款 元;在乙店购买需付款 元。
(2)当购买乒乓球盒数为10盒时,若只能选择一家商店去购买,到哪家商店购买比较合算?并说明理由。
(3)当购买乒乓球盒数为10盒时,若不限制购买的商店,请你给出一种更为省钱的购买方案,并求出此时需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.

(1).请用两种不同的方法表示图中阴影部分的面积.
方法①: ;
方法②: .
(2).由 (1)可得出![]() 2,
2,![]() ,4mn这三个代数式之间的一个等量关系为: .
,4mn这三个代数式之间的一个等量关系为: .
(3)利用(2)中得到的公式解决问题:已知2a+b=6,ab=4,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3 , 现有如下结论:
①S1:S2=AC2:BC2;
②连接AE,BD,则△BCD≌△ECA;
③若AC⊥BC,则S1S2= ![]() S32 .
S32 .
其中结论正确的序号是 . 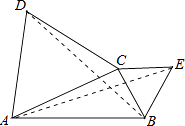
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com