
【题目】我们定义:
在一个三角形中,如果一个角的度数是另一个角的度数![]() 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为
倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为![]() ,
,![]() ,
,![]() 的三角形是“和谐三角形”
的三角形是“和谐三角形”
概念理解:
如图,![]() ,在射线
,在射线![]() 上找一点
上找一点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,以
,以![]() 为端点作射线
为端点作射线![]() ,交线段
,交线段![]() 于点
于点![]() (点
(点![]() 不与
不与![]() 重合)
重合)

(1)![]() 的度数为 ,
的度数为 ,![]() (填“是”或“不是”)“和谐三角形”
(填“是”或“不是”)“和谐三角形”
(2)若![]() ,求证:
,求证:![]() 是“和谐三角形”.
是“和谐三角形”.
应用拓展:
如图,点![]() 在
在![]() 的边
的边![]() 上,连接
上,连接![]() ,作
,作![]() 的平分线
的平分线![]() 交于点
交于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,
,![]() .若
.若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() 的度数.
的度数.

【答案】(1)![]() °,是;(2)见解析;(3)
°,是;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)根据垂直的定义、三角形内角和定理求出∠ABO的度数,根据“和谐三角形”的概念判断;
(2)根据三角形外角的性质求出![]() 的度数,然后根据“和谐三角形”的概念证明即可;
的度数,然后根据“和谐三角形”的概念证明即可;
应用拓展:首先易证∠EFC=∠ADC,根据平行线的性质得到∠DEF=∠ADE,推出DE∥BC,得到∠CDE=∠BCD,根据角平分线的定义得到∠ADE=∠CDE,求得∠B=∠BCD,然后根据“和谐三角形”的定义求解即可.
解: (1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为“和谐三角形”,
为“和谐三角形”,
故答案为:![]() °;是;
°;是;
(2)证明:∵![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是“和谐三角形”;
是“和谐三角形”;
应用拓展:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是“和谐三角形”,
是“和谐三角形”,
∴![]() ,或
,或![]() ,
,
∵![]() ,
,
∴![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在某建筑物AC上,挂着一宣传条幅BC,站在点F处,测得条幅顶端B的仰角为300,往条幅方向前行20米到达点E处,测得条幅顶端B的仰角为600,求宣传条幅BC的长.(![]() ,结果精确到0.1米)
,结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3,
(1)用描点法画出y=x2+2x﹣3的图象.
(2)根据你所画的图象回答问题:当x 时,函数值y随x的增大而增大,当x 时,函数值y随x的增大而减小.
解:列表得:
X | |||||||
Y |
描点、连线

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.
(1)求甲、乙2名学生在不同书店购书的概率;
(2)求甲、乙、丙3名学生在同一书店购书的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.求:

(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图12,在△ABC中,∠C=90°,AB=10cm,BC=6cm. 点P从点A出发,沿AB边以2 cm/s的速度向点B匀速移动;点Q从点B出发,沿BC边以1 cm/s的速度向点C匀速移动. 当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,QB=QP;
(3)当t为何值时,△PBQ的面积等于4.8cm 2.
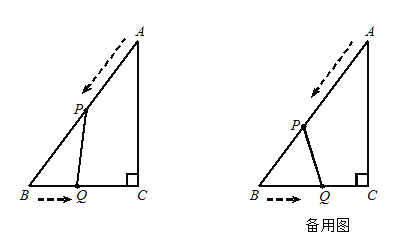
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:

(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作
y轴的平行线,与直线AC交于点G(点G在点F的上方).若, ![]()
求点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com