
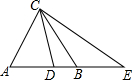
 如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.
如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.分析 (1)根据相似三角形的判定证明即可;
(2)利用相似三角形的性质解答即可.
解答 证明:(1)∵AB=AC,
∴∠ACB=∠ABC,
∵∠ECB=∠DCB,
∴∠ACB-∠DCB=∠ABC-∠ECB,
∵∠ACD=∠ACB-∠DCB,∠AEC=∠ABC-∠ECB,
∴∠ACD=∠AEC,
∵∠A=∠A,
∴△ADC~△ACE;
(2)∵△ADC~△ACE,
∴$\frac{AD}{AC}=\frac{AC}{AE}$,
∴$AD=\frac{A{C}^{2}}{AE}=\frac{{8}^{2}}{12}=\frac{16}{3}$,
∴BD=AB-AD=$8-\frac{16}{3}=\frac{8}{3}$.
点评 此题考查相似三角形的判定和性质问题,关键是根据相似三角形的判定证明.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
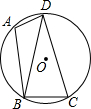 如图,己知四边形ABCD内接于圆O,连结BD,∠BAD=115°,∠DBC=65°.
如图,己知四边形ABCD内接于圆O,连结BD,∠BAD=115°,∠DBC=65°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-2且x≠0 | B. | x>0 | C. | -2≤x<0 | D. | 0<x≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
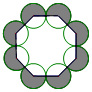 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com