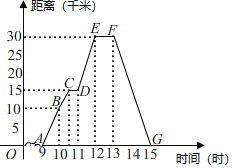
【题目】如图所示表示王勇同学骑自行车离家的距离与时间之间的关系，王勇9点离开家，15点回家，请结合图象，回答下列问题：
到达离家最远的地方是什么时间？离家多远？
他一共休息了几次？休息时间最长的一次是多长时间？
在哪些时间段内，他骑车的速度最快？最快速度是多少？
科目：初中数学 来源： 题型：
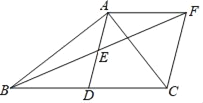
【题目】如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．
（1）求证：△AEF≌△DEB；
（2）若∠BAC=90°，试判断四边形ADCF的形状，并证明你的结论；
（3）在（2）的情况下，点M在AC线段上移动，请直接回答，当点M移动到什么位置时，MB+MD有最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）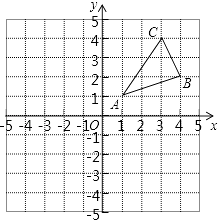 
．
（1）请画出△ABC关于原点对称的△A2B2C2；并写出各点的坐标．
（2）在x轴上求作一点P，使△PAB的周小最小，请画出△PAB，并直接写出P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是cm． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
中，
，将线段AB绕点A按逆时针方向旋转
得到线段AD，其中
连结BD，CD，
．
若
，
，在图1中补全图形，并写出m值．
如图2，当
为钝角，
时，m值是否发生改变？证明你的猜想．
如图3，
，
，BD与AC相交于点O，求
与
的面积比．
查看答案和解析>>
科目：初中数学 来源： 题型：
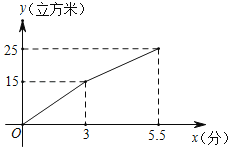
【题目】某种水泥储存罐的容量为25立方米，它有一个输入口和一个输出口．从某时刻开始，只打开输入口，匀速向储存罐内注入水泥，3分钟后，再打开输出口，匀速向运输车输出水泥，又经过2.5分钟储存罐注满，关闭输入口，保持原来的输出速度继续向运输车输出水泥，当输出的水泥总量达到8立方米时，关闭输出口．储存罐内的水泥量y（立方米）与时间x（分）之间的部分函数图象如图所示．
（1）求每分钟向储存罐内注入的水泥量．
（2）当3≤x≤5.5时，求y与x之间的函数关系式．
（3）储存罐每分钟向运输车输出的水泥量是 立方米，从打开输入口到关闭输出口共用的时间为 分钟．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市某中学有一块四边形的空地ABCD，如图所示，为了绿化环境，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，DA=4m，BC=12m，CD=13m．
（1）求出空地ABCD的面积．
（2）若每种植1平方米草皮需要200元，问总共需投入多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，反比例函数y= 
（x＞0）的图象经过点A（2 
，1），射线AB与反比例函数图象交与另一点B（1，a），射线AC与y轴交于点C，∠BAC=75°，AD⊥y轴，垂足为D．
（1）求k和a的值；
（2）直线AC的解析式；
（3）如图3，M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC相交于N，连接CM，求△CMN面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们来定义一种新运算：对于任意实数x、y，“※”为a※b=（a+1）（b+1）﹣1
（1）计算（﹣3）※9
（2）嘉琪研究运算“※”之后认为它满足交换律，你认为她的判断 （正确、错误）
（3）请你帮助嘉琪完成她对运算“※”是否满足结合律的证明．
证明：由已知把原式化简得a※b=（a+1）（b+1）﹣1=ab+a+b
∵（a※b）※c=（ab+a+b）※c=
a※（b※c）=
∴
∴运算“※”满足结合律．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
