
【题目】如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若![]() +|y-80-m|+|z-40|=0(m为常数,且0<m<100)
+|y-80-m|+|z-40|=0(m为常数,且0<m<100)
(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数


【答案】(1) ∠A=m+20°,∠C=m+80°;(2)见解析; (3)50°、70°、30°、10°.
【解析】
(1)根据二次根式和绝对值的非负数性质解答即可;(2)过点F作FG∥AB,过点E作EH∥AB,可知EH//FG,根据平行线性质可证明∠BAE=∠AEH=m+20°,∠EFG=∠FEH,进而证明∠EFG=∠AEF-∠AEH=80°-(m+20°)=60°-m,由∠CFG+∠FCD=y+z+80°-x=80°+m+40°+80°-m-20°=180°,通过判定定理即可证明结论;(3)当∠A=40°时,∠C=100°,分情况讨论AM和FM的位置,计算即可;
(1) ∵![]() +|y-80-m|+|z-40|=0(m为常数,且0<m<100),
+|y-80-m|+|z-40|=0(m为常数,且0<m<100),
∴x-m-20=0,y-80-m=0,z-40=0,
∴∠A=x°=m+20°,∠C=y°=m+80°,z=40°,
(2) 过点F作FG∥AB,过点E作EH∥AB,
∴EH∥FG,
∴∠BAE=∠AEH=m+20°,∠EFG=∠FEH,
∴∠EFG=∠AEF-∠AEH=80°-(m+20°)=60°-m,
∵∠CFG+∠FCD=y+z+80°-x=80°+m+40°+80°-m-20°=180°,
∴AB∥CD,
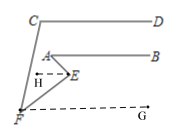
(3) 当∠A=40°时,∠C=100°,
如图,分为四种情况:
延长FE交AM于N,
∵∠BAE=40°,∠BAM=20°,
∴∠MAE=20°,
∵∠AEF=80°,
∴∠ANE=80°-20°=60°,
∴∠AMF=60°-10°=50°,
∵∠AGF=∠MFE+∠AEF=10°+80°=90°,
∴∠AMF=90°-∠MAE=70°,
∵∠BAM=20°,∠BAE=40,°
∴∠EAM=60°,
∵∠AHF=∠MFE+∠AEF=90°,
∴∠AMF=90°-∠EAM=30°,
延长AE交FM于O,
∵∠AEF=∠EFO+∠AOF=80°,
∴∠AOF=80°-10°=70°,
∴∠AMF=∠AOF-∠MAF=70°-60°=10°,
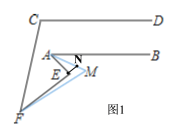
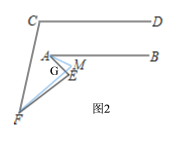
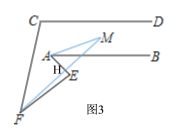
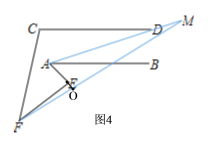
综上所述:∠AMF的度数分别为:50°;70°;30°;10°.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AP垂直∠ABC的平分线BP于点P.若△ABC的面积为32cm2,BP=6cm,且△APB的面积是△APC的面积的3倍.则AP=________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如图两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题. 
(1)m=%,这次共抽取名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H. 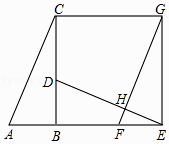
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,A(a,3)、B(b,6)、C(c,1),a、b、c都为实数,并且满足3b-5c=-2a-18,4b-c=3a+10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时,判断△ABC的面积是否发生变化?若不变,求其值;若变化,求其变化范围
(3) 当实数a变化时,若线段AB与y轴相交,线段OB与线段AC交于点P,且S△PAB>S△PBC,求实数a的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xoy中,抛物线y=(m﹣1)x2﹣(3m﹣4)x﹣3与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴是经过(1,0)且与y轴平行的直线,点P是抛物线上的一点,点Q是y轴上一点;
(1)求抛物线的函数关系式;
(2)若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)若tan∠PCB= ![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
(1)化简并求值:-(3a2-4ab)+[a2-![]() (a+2ab)] ,其中a=-2,b=1
(a+2ab)] ,其中a=-2,b=1
(2)已知多项式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求a、b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com