
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,取斜边AB的中点E,易得△BCE是等边三角形,从而得到“直角三角形中,30°角所对的直角边等于斜边的一半”利用这个结论解决问题:
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,若动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A.B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
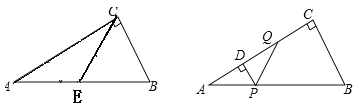
【答案】(1)![]() ;(2)t的值为
;(2)t的值为![]() 或
或![]() 或
或![]()
【解析】
(1)在Rt△ABC中,利用结论可得![]() ,可由勾股定理求出AC,在Rt△ADP中,由题意AP=2t,PD=t,用勾股定理可表示出AD,再用DC=AC-AD即可;
,可由勾股定理求出AC,在Rt△ADP中,由题意AP=2t,PD=t,用勾股定理可表示出AD,再用DC=AC-AD即可;
(2)分三种情况讨论,①当PQ的垂直平分线与PQ交于点G,且经过AB的中点F时,易证△PAD≌QPD,△PFG≌PAD,可得PF=AP=2t,而F为AB的中点,利用AP+PF=![]() AB可求t;
AB可求t;
②当PQ的垂直平分线经过AC的中点M时,可在Rt△MGQ中,求出MQ,然后利用AM+MQ=2AD可求出t;
③当PQ的垂直平分线经过BC的中点N,与AB的延长线交于H点时,
易证△PHG≌△PAD,则PH=AP=2t,然后利用等角对等边得到BH=BN=1,再由AH=AB+BN可求出t.
(1)在Rt△ABC中,利用结论可得![]() ,
,
∴![]()
在Rt△ADP中,由题意AP=2t,PD=t,
∴![]() ,
,
∴![]()
∵点P不与点A.B重合,∴![]()
故![]() .
.
(2)①当PQ的垂直平分线与PQ交于点G,且经过AB的中点F时,如图1,

在△APD和△QPD中,

∴![]()
∴PA=PQ,∠PQD=∠A=30°,AD=QD=![]()
∵GF是PQ的中垂线,∴![]() ,
,
在△APD和△FPG中,

∴![]()
∴PA=PF=2t
∵F为AB中点,∴AF=PA+PF=![]() AB,
AB,
即2t+2t=2,解得t=![]()
②当PQ的垂直平分线经过AC的中点M时,如图2,

由①可知PG=QG=![]() PQ=t,
PQ=t,
在Rt△MGQ中,设MG=x,∵∠MQG=30°,∴MQ=2x
由勾股定理得![]()
即![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
∴![]() ,
,
∵M为AC的中点,∴AM=![]() AC=
AC=![]() ,
,
AM+MQ=2AD,即![]() +
+![]() =
=![]() ,解得t=
,解得t=![]()
③当PQ的垂直平分线经过BC的中点N,与AB的延长线交于H点时,如图3,

在Rt△PFG中,![]() ,
,
∵∠ABC=∠H+∠BNH=60°,∴∠BNH=∠H=30°,∴BH=BN=![]() =1
=1
同①可证△PHG≌△PAD,∴PH=PA=2t,
由AB+BH=PA+PH=2PA得4+1=4t,解得t=![]()
综上,当线段PQ的垂直平分线经过△ABC一边中点时,t的值为![]() 或
或![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )

A. 3 B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,AB=50km,A、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图1是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB,图2是方案二的示意图(点A关于直线X的对称点是A',连接BA′交直线X于点P),P到A、B的距离之和S2=PA+PB

(1)S1=_____km.S2=_____km.
(2)PA+PB的最小值为_____km.
(3)拟建的恩施到张家界高速公路与沪渝高速公路垂直,建立如图3所示的直角坐标系,B到直线的距为30km,请你在X旁和P旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小,(用尺画出点P和点Q的位置)这个最小值为_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A.将y=
(x>0)的图象交于点A.将y=![]() x的图象向下移6个单位后与双曲线y=
x的图象向下移6个单位后与双曲线y=![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求点C的坐标;
(2)若![]() =2,求反比例函数的表达式.
=2,求反比例函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
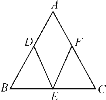
【题目】如图,△ABC中,AB=AC,点D,E,F分别是△ABC边AB,BC,AC的中点,连接DE,EF,要使四边形ADEF是正方形,还需增加条件:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶![]() ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )

A. 15米 B. 20![]() 米 C. 20
米 C. 20![]() 米 D. 10
米 D. 10![]() 米
米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com