练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．若∠AOB=50°，∠BOC=30°，则∠AOC=20°或80；若OM是∠AOB的平分线，ON是∠BOC的平分线，则∠MON=40°或10°．

    分析 根据题意画出图形，进而利用角平分线的定义求出即可．

    解答 解：如图所示：
    ∵∠AOB=50°，∠BOC=30°，
    ∴∠AOC′=∠AOB+∠BOC=80°，
    或∠AOC=∠AOB-∠BOC=20°，
    故∠AOC=20°或80°，
    ∵OM是∠AOB的平分线，ON是∠BOC的平分线，
    ∴∠MON′=$\frac{1}{2}$∠AOC′或∠MON=$\frac{1}{2}$∠AOC，
    故∠MON=40°或10°．
    故答案为：20°或80；40°或10°．

    点评 此题主要考查了角平分线的定义以及角的计算，利用分类讨论得出是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．画出y=$\frac{1}{2}$x2-6x+3的图象（草图），并写出其顶点坐标、对称轴和最值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．阅读下列材料，然后回答问题．在进行二次根式的化简运算时，我们有时会碰上形如$\frac{2}{\sqrt{3}+1}$的式子，其实我们还可以将其进一步简化：$\frac{2}{\sqrt{3}+1}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}）^{2}-{1}^{2}}$=$\sqrt{3}$-1．以上这种化简的步骤叫做分母有理化．
    请用上面的方法化简：$\frac{1}{2-\sqrt{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

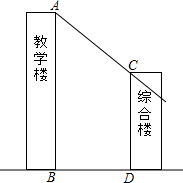    18．如图所示，综合楼高12m，两楼相距5m，在下午某一时刻太阳光与水平面的夹角为30°，当教学楼影子顶端A刚好落在综合楼顶端C处时，问教学楼的高度约为多少米？（$\sqrt{3}$≈1.732，结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图所示，平面直角坐标系中画出了一次函数y=-2x=2和一次函数y=kx+b的图象．
    （1）求一次函数y=kx+b的解析式；
    （2）求方程组$\left\{\begin{array}{l}{y=-2x+2}\\{y=kx+b}\end{array}\right.$的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

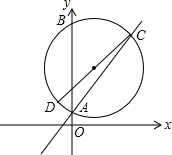    15．如图，半径为5的⊙O1，交直线y=x+2于A（0，2），C两点，交y轴与B（0，10），CD是⊙O1的直径，若函数y=$\frac{k}{x}$（x＜0）的图象经过点D，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

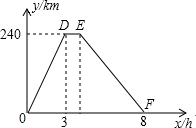    2．小王从A地前往B地送货，到达B地后，休息1h后按原路返回，他与A地的距离y（单位：km）和所用的时间x（单位；h）之间的函数关系式如图所示．
    （1）小王从B地返回A地的速度是多少？
    （2）在A，B之间有一个C地，小王从去时途径C地到返回时路过C地，公用了4.5h，那么A，C两地相距多远？
    （3）小李在小王出发2h后，按小王大的路线也从A地前往B地，行驶路程为216km/时，在小王返回途中两人相遇，问小李行驶了多长时间？直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．求一次函数y=$\frac{1}{2}$x-1的图象与一次函数y=-x-3的图象的交点坐标，并求出这两个函数的图象与x轴所围成的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．探究：中华人民共和国国旗上的五角星的每个角均相等，小明为了计算每个角的度数，画出了如图①的五角星，每个角均相等，并写出了如下不完整的计算过程，请你将过程补充完整．
    解：∵∠AFG=∠C+∠E，∠AGF=∠B+∠D．
    ∴∠AFG+∠AGF=∠C+∠E+∠B+∠D．
    ∵∠A+∠AFG+∠AGF=180°，
    ∴∠A+∠B+∠C+∠D+∠E=180°，
    ∴∠A=∠B=∠C=∠D=∠E=36°．
    拓展：如图②，小明改变了这个五角星的五个角的度数，使它们均不相等，请你帮助小明求∠A、∠B、∠C、∠D、∠E的和．
    应用：如图③．小明将图②中的点A落在BE上，点C落在BD上，若∠B=∠D=36°，则∠CAD+∠ACE+∠E=108°．

    查看答案和解析>>

    同步练习册答案