
 如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.
如图,直线y=2x+2交y轴于A点,交x轴于C点,以O,A,C为顶点作矩形OABC,将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,直线AC交直线DF于G点.分析 (1)根据直线的解析式找出点A、C的坐标,再由旋转的特性找出点D、F的坐标,结合点D、F的坐标利用待定系数法即可求出直线DF的解析式;
(2)过点O作OP⊥AC于点P,作OQ⊥DG于点Q,利用全等直角三角形的判定定理HL证出Rt△OAC≌Rt△ODF,结合面积法即可得出OP=OQ,从而证出GO平分∠CGD;
(3)根据旋转的性质可得出AC⊥DF,结合(2)的结论即可得出∠OGD=45°,联立直线AC、DF的解析式成方程组,解方程组可得出点G的坐标,根据等腰直角三角形的性质可分两种情况寻找点M的位置,再通过勾股定理解方程等即可得出结论.
解答 解:(1)∵直线y=2x+2交y轴于A点,交x轴于C点,
∴A点的坐标是(0,2),C点的坐标是(-1,0),
∵将矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,
∴F点的坐标是(0,1),D点的坐标是(2,0),
设直线DF的解析式是y=kx+1,
∴2k+1=0,
解得k=-$\frac{1}{2}$,
∴直线DF的解析式是:y=-$\frac{1}{2}$x+1.
(2)过点O作OP⊥AC于点P,作OQ⊥DG于点Q,如图1所示.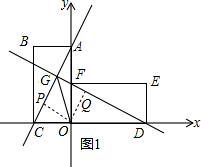
在Rt△OAC和Rt△ODF中,$\left\{\begin{array}{l}{OA=OD}\\{AC=DF}\end{array}\right.$,
∴Rt△OAC≌Rt△ODF(HL),
又∵OP⊥AC,OQ⊥DG,
∴OP=OQ,
∴OG平分∠CGD.
(3)∵矩形OABC绕O点顺时针旋转90°,得到矩形ODEF,
∴对角线AC⊥DF,
∵GO平分∠CGD,
∴∠OGD=45°.
解$\left\{\begin{array}{l}{y=2x+2}\\{y=-\frac{1}{2}x+1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=-\frac{2}{5}}\\{y=\frac{6}{5}}\end{array}\right.$,
即点G(-$\frac{2}{5}$,$\frac{6}{5}$),
∴直线GO为y=-3x.
∵D(2,0),
∴GD=$\sqrt{[2-(-\frac{2}{5})]^{2}+(0-\frac{6}{5})^{2}}$=$\frac{6\sqrt{5}}{5}$,GO=$\sqrt{(-\frac{2}{5}-0)^{2}+(\frac{6}{5}-0)^{2}}$=$\frac{2\sqrt{10}}{5}$.
以点G、M、D为顶点的三角形是等腰直角三角形分两种情况:
①过D作DM1⊥GO于点M1,则△GM1D是以GD为斜边的等腰直角三角形,过M1作M1H⊥OD于点H,如图2所示.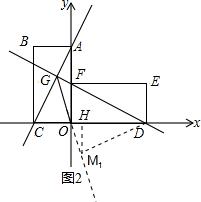
∵GD=$\frac{6\sqrt{5}}{5}$,
∴GM1=DM1=$\frac{6\sqrt{5}}{5}$×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{10}}{5}$.
∵GO=$\frac{2\sqrt{10}}{5}$,
∴OM1=GM1-GO=$\frac{3\sqrt{10}}{5}$-$\frac{2\sqrt{10}}{5}$=$\frac{\sqrt{10}}{5}$.
设点M1(x,-3x),在Rt△OM1H中有$O{H}^{2}+H{{M}_{1}}^{2}=O{{M}_{1}}^{2}$,
即x2+(-3x)2=$(\frac{\sqrt{10}}{5})^{2}$,解得:x=$\frac{1}{5}$或x=-$\frac{1}{5}$(舍去).
∴点M1($\frac{1}{5}$,-$\frac{3}{5}$);
②过D作DM2⊥GD交GO于M2,则△GM2D是以GD为直角边的等腰直角三角形,过M2作M2I⊥OD于点I,如图3所示.
∵GD=$\frac{6\sqrt{5}}{5}$,
∴GM2=$\frac{6\sqrt{5}}{5}$×$\sqrt{2}$=$\frac{6\sqrt{10}}{5}$,
∵GO=$\frac{2\sqrt{10}}{5}$,
∴OM2=GM2-GO=$\frac{6\sqrt{10}}{5}$-$\frac{2\sqrt{10}}{5}$=$\frac{4\sqrt{10}}{5}$.
设M2(a,-3a),在Rt△OM2I中有$O{I}^{2}+I{{M}_{2}}^{2}=O{{M}_{2}}^{2}$,
即a2+(-3a)2=$(\frac{4\sqrt{10}}{5})^{2}$,解得:a=$\frac{4}{5}$或a=-$\frac{4}{5}$(舍去),
∴点M2($\frac{4}{5}$,-$\frac{12}{5}$).
综上可得:使以点G、M、D为顶点的三角形是等腰直角三角形的M点的坐标为($\frac{1}{5}$,-$\frac{3}{5}$)和($\frac{4}{5}$,-$\frac{12}{5}$).
点评 本题考查了旋转的性质、待定系数法求函数解析式、全等三角形的判定及性质、等腰直角三角形的性质以及勾股定理,解题的关键是:(1)利用待定系数法求函数解析式;(2)证出Rt△OPG≌Rt△OQG;(3)分情况讨论点M的情况.本题属于中档题,难度不大,但解题过程稍显繁琐,解决该题型题目时,根据旋转的性质找出点的坐标,再利用待定系数法求出函数解析式是关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
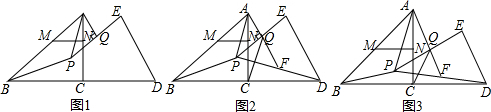
 如图,边长为4的等边△ABC和等边△DEF互相重合,现将△ABC沿直线l向左平移m个单位,将△DEF沿直线l向右平移m个单位.
如图,边长为4的等边△ABC和等边△DEF互相重合,现将△ABC沿直线l向左平移m个单位,将△DEF沿直线l向右平移m个单位.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com