
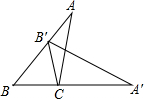
 如图,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′处,此时,点A的对应点A′恰好落在BC边的延长线上,下列结论错误的是( )
如图,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′处,此时,点A的对应点A′恰好落在BC边的延长线上,下列结论错误的是( )| A. | ∠BCB′=∠ACA′ | B. | ∠ACB=2∠B | C. | ∠B′CA=∠B′AC | D. | B′C平分∠BB′A′ |
分析 根据旋转的性质得到∠BCB′=∠ACA′,故A正确,根据等腰三角形的性质得到∠B=∠BB'C,根据三角形的外角的性质得到∠A'CB'=2∠B,等量代换得到∠ACB=2∠B,故B正确;等量代换得到∠A′B′C=∠BB′C,于是得到B′C平分∠BB′A′,故D正确.
解答 解:根据旋转的性质得,∠BCB'和∠ACA'都是旋转角,则∠BCB′=∠ACA′,故A正确,
∵CB=CB',
∴∠B=∠BB'C,
又∵∠A'CB'=∠B+∠BB'C,
∴∠A'CB'=2∠B,
又∵∠ACB=∠A'CB',
∴∠ACB=2∠B,故B正确;
∵∠A′B′C=∠B,
∴∠A′B′C=∠BB′C,
∴B′C平分∠BB′A′,故D正确;
故选C.
点评 本题考查了旋转的性质,角平分线的定义,等腰三角形的性质,正确的识别图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com