
【题目】问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c=①______,
因为c=13,所以a+b=②______,
所以(a+b)2=③______,所以a2+ b2+④_____=289.
因为a2+b2=c2,所以c2+2ab=289,
所以⑤______+2ab=289,所以ab=⑥______(第1步),
所以△ABC的面积=![]() ab=
ab=![]() ×⑦______=⑧______(第2步).
×⑦______=⑧______(第2步).
合作探究:(1)对解法展示进行填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是______(填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
【答案】(1)①30,②17,③172(或289),④2ab,⑤132(或169),⑥ab=60,⑦60,⑧30;(2)①;(3)这个直角三角形的周长是24.
【解析】
(1)根据三角形的周长定义,勾股定理,三角形的面积公式即可求解;
(2)根据(1)的解答过程得到由第1步到第2步体现出来的数学思想是整体思想;
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数).利用勾股定理和三角形的面积公式求得两直角边是6和8.然后由三角形的周长公式求得该直角三角形的周长.
(1) 设Rt△ABC的两直角边长分别为a,b,则a+b+c=①___30___,
因为c=13,所以a+b=②___17___,
所以(a+b)2=③___172(或289)___,所以a2+ b2+④_2ab ___=289.
因为a2+b2=c2,所以c2+2ab=289,
所以⑤___132(或169)___+2ab=289,所以ab=⑥____60__(第1步),
所以△ABC的面积=![]() ab=
ab=![]() ×⑦___60___=⑧__30____(第2步).
×⑦___60___=⑧__30____(第2步).
(2) 根据(1)的解答过程得到由第1步到第2步体现出来的数学思想是整体思想,故选①;
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数),则依题意得:

解得![]()
所以这个直角三角形的周长是:6+8+10=24.
∴这个直角三角形的周长是24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】全国两会民生话题成为社会焦点,我市记者为了解百姓“两会民生话题”的聚焦点,随机调查了我市部分市民,并对调查结果进行整理,绘制了如图所示的两幅不完整的统计图表.
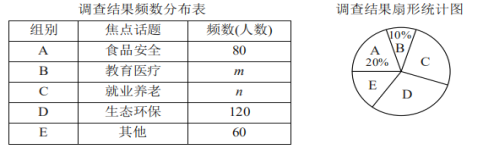
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 %;
(2)我市人口现有650万,请你估计其中关注D组话题的市民人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.
与x轴,y轴分别交于点A,B,将直线AB向右平移6个单位长度,得到直线CD,点A平移后的对应点为点D,点B平移后的对应点为点C.
(1)求点C的坐标;
(2)求直线CD的表达式;
(3)若点B关于原点的对称点为点E,设过点E的直线![]() ,与四边形ABCD有公共点,结合函数图象,求k的取值范围.
,与四边形ABCD有公共点,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是____.
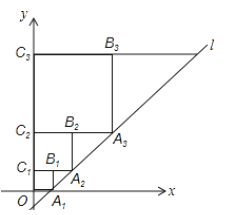
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,∠D=60°,AB=4,E为边BC上的动点,连接AE,作AE的垂直平分线GF交直线CD于F点,垂足为点G,则线段GF的最小值为____________.
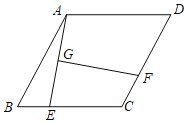
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 75 | |
乙 | 78 | 80.5 |
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
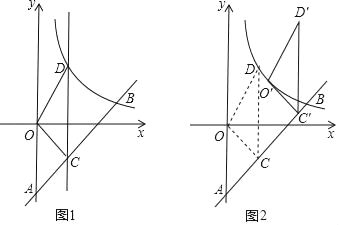
【题目】如图1,一次函数y=kx﹣6(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上一点,过点C且平行于y轴的直线l交该反比例函数的图象于点D,连接OC,OD,BD,若四边形OCBD的面积S四边形OCBD=![]() ,求点C的坐标;
,求点C的坐标;
(3)将第(2)小题中的△OCD沿射线AB方向平移一定的距离后,得到△O'C'D',若点O的对应点O'恰好落在该反比例函数图象上(如图2),求此时点D的对应点D'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
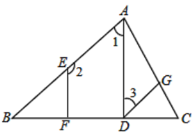
【题目】学着说点理:补全证明过程:
如图,已知![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .请补充证明过程,并在括号内填上相应的理由.
.请补充证明过程,并在括号内填上相应的理由.
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (___________________),
(___________________),
∴![]() (___________________),
(___________________),
∴________![]() (___________________).
(___________________).
又∵![]() (已知),
(已知),
∴![]() (___________________),
(___________________),
∴![]() ________(___________________),
________(___________________),
∴![]() (___________________).
(___________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com