
已知:如图4346,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD∶AB=__________时,四边形MENF是正方形(只写结论,不需证明).
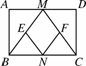
(1)证明:在矩形ABCD中,
AB=CD,∠A=∠D=90°,
又∵M是AD的中点,∴AM=DM.
∴△ABM≌△DCM(SAS).
(2)解:四边形MENF是菱形.证明如下:
E,F,N分别是BM,CM,CB的中点,
∴NE∥MF,NE=MF.
∴四边形MENF是平行四边形.
由(1),得BM=CM,∴ME=MF.
∴四边形MENF是菱形.
(3)2∶1 解析:当AD∶AB=2∶1时,四边形MENF是正方形.理由:
∵M为AD中点,∴AD=2AM.
∵AD∶AB=2∶1,∴AM=AB.
∵∠A=90,∴∠ABM=∠AMB=45°.
同理∠DMC=45°,∴∠EMF=180°-45°-45°=90°.
∵四边形MENF是菱形,∴菱形MENF是正方形.


科目:初中数学 来源: 题型:
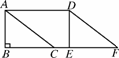
如图4341,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.将△ABC沿射线BC方向平移10 cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
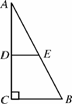
如图4358,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
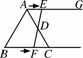
如图4365,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,同时点F从点B出发沿射线BC以2 cm/s的速度运动,设运动时间为t(单位:s).
(1)连接EF,当EF经过AC边的中点D时,求证: △ADE≌△CDF.
(2)填空:
①当t为________s时,四边形ACFE是菱形;
②当t为________s时,以A,F,C,E为顶点的四边形是直角梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中:①所有的等腰三角形都相似;②所有的正三角形都相似;③所有的正方形都相似;④所有的矩形都相似.其中说法正确的序号是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com