
【题目】如图所示,已知抛物线y=ax2+bx+c过点A(﹣1,0),且经过直线y=x﹣3与坐标轴的两个交点B、C.
(1)求抛物线的表达式;
(2)若点M在第四象限内且在抛物线上,有OM⊥BC,垂足为D,求点M的坐标.

【答案】(1)y=x2﹣2x﹣3;(2)M点坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】【试题分析】
(1)先求出y=x﹣3与x轴的交点B的坐标为(3,0),与y轴的交点C的坐标为(0,﹣3),A点坐标为(﹣1,0),用交点式设二次函数解析式为y=a(x+1)(x﹣3),将C(0,﹣3)代入解析式得,﹣3=a×1×(﹣3),解得,a=1,则y=(x+1)(x﹣3),化为一般式得:y=x2﹣2x﹣3,
(2)由于OD过原点,则OD为正比例函数的图像,设OD的解析式为y=kx,
因为OM⊥BC,BC解析式为y=x-3,根据两条垂直的一次函数的k值互为相反数,得:
kOD=﹣1,则OD的解析式为y=﹣x,将y=x2﹣2x﹣3和y=﹣x组成方程组得![]() ,
,
解得,x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
把x1=![]() 代入y=﹣x得,y1=﹣
代入y=﹣x得,y1=﹣![]() ,
,
即M点坐标为(![]() ,﹣
,﹣![]() ).
).
【试题解析】
(1)∵y=x﹣3与x轴的交点B的坐标为(3,0),与y轴的交点C的坐标为(0,﹣3),A点坐标为(﹣1,0),
∴设二次函数解析式为y=a(x+1)(x﹣3),
将C(0,﹣3)代入解析式得,
﹣3=a×1×(﹣3),
解得,a=1,
则二次函数解析式为y=(x+1)(x﹣3),
即y=x2﹣2x﹣3,
(2)∵OD过原点,
∴设OD的解析式为y=kx,
∵OM⊥BC,BC解析式为y=x﹣3,
∴kOD=﹣1,
则OD的解析式为y=﹣x,
将y=x2﹣2x﹣3和y=﹣x组成方程组得![]() ,
,
整理得,x2﹣x﹣3=0,
解得,x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
把x1=![]() 代入y=﹣x得,
代入y=﹣x得,
y1=﹣![]() ,
,
∴M点坐标为(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的图形△![]() .
.
(2)画出△ABC关于点O的中心对称图形 △![]() .
.
(3)△![]() 与△
与△![]() 组成的图形__________ 轴对称图形. (填“是”或“不是”)
组成的图形__________ 轴对称图形. (填“是”或“不是”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]()
![]() 交于A点,且点A的横坐标是4.双曲线
交于A点,且点A的横坐标是4.双曲线![]()
![]() 上有一动点C(m,n),
上有一动点C(m,n), ![]() .过点A作
.过点A作![]() 轴垂线,垂足为B,过点C作
轴垂线,垂足为B,过点C作![]() 轴垂线,垂足为D,联结OC.
轴垂线,垂足为D,联结OC.

(1)求![]() 的值;
的值;
(2)设![]() 的重合部分的面积为S,求S与m的函数关系;
的重合部分的面积为S,求S与m的函数关系;
(3)联结AC,当第(2)问中S的值为1时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?
(解析)解:BE∥DF.
∵AB⊥BC,
∴∠ABC= °,
即∠3+∠4= °.
又∵∠1+∠2=90°,
且∠2=∠3,
∴ = .
理由是: .
∴BE∥DF.
理由是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
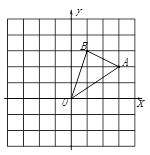
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的的坐标分别为A(3,2)、B(1,3).
⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1,点B1的坐标为 ;
⑵.请画出将△AOB关于原点O成对称的图形△A2OB2,点A2的坐标为 ;
⑶.在x轴上找一点P,使PA+PB的值最小,则P点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月30日上午符离大道正式开通,同时宿州至徐州的K902路城际公交开通试运营,小明先乘K902路城际公交车到五柳站下车,再步行到五柳景区游玩,从出发地到五柳景区全程31千米,共用了1个小时,已知步行的速度每小时4千米,K902路城际公交的速度是步行速度的10倍,求小明乘公交车所行驶的路程和步行的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体育活动”,决定开展以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次活动一共调查了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于多少度?
(4)若该学校有2500人,请你估计该学校选择羽毛球项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
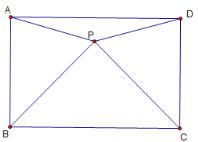
【题目】如图,P 为平行四边形 ABCD 内一点,PB=PC,∠BPC=90°,∠PAB=75°,若 AB=11![]() ,PD=14,则 PA 的长为_______________.
,PD=14,则 PA 的长为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com