【题目】如图1，在正方形ABCD中，M是AD的中点，点E是边AB上的一个动点，连接EM并延长交射线CD于点F，过点M作EF的垂线交射线BC于点G，连结EG、FG．
求证：
≌
；
．
在点E的运动过程中，探究：
的值是否发生变化？若不变，求出这个值；
如图2，把正方形ABCD改为矩形
，
，
，其他条件不变，当
为等边三角形时，试求k的值．
【答案】
证明见解析；
证明见解析；
的值不变，值为2；
．
【解析】
（1）
根据正方形性质得
．
．又
，可证
≌
；
；（2）
的值不变．如图1，过点G作
，垂足为点N，由矩形性质，证∽
，得
，所以，
为定值不变；如图2，过点G作，垂足为点N，由四边形ABGN是矩形．
．由等边三角形性质，得
，同的方法得，∽，
，
是AD的中点，
，可求得k.
四边形ABCD是正方形，
．
是AD的中点，
．
又
，
≌；
由≌
，
．
，
；
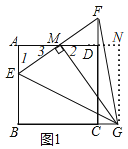
的值不变．
如图1，过点G作，垂足为点N，
则四边形ABGN是矩形．
．
，
．
在
中，
，
．
．
∽，
，
为定值不变；
如图2，过点G作，垂足为点N，
则四边形ABGN是矩形．
．
若
是等边三角形，则，
同的方法得，∽，
，
是AD的中点，
，
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD是边长为3的正方形，动点P从点B出发，沿BC向终点C运动，点P可以与点B、点C重合，连接PD，将
沿直线PD折叠，设折叠后点C的对应点为点E，连接AE并延长交BC于点F，连接BE，则下列结论中：
当
时，
为等边三角形；
当时，F为BC的中点；
当
时，
；
当点P从点B运动到点C时，点E所走过的路径的长为
其中正确的有
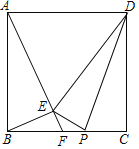
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践
（1）观察理解：如图1，
中，
，
，直线
过点
，点
，
在直线同侧，
，
，垂足分别为
，
，由此可得：
，所以
，又因为，所以
，所以
，又因为，所以
（ ）；（请填写全等判定的方法）
（2）理解应用：如图2，
，且
，
，且
，利用（1）中的结论，请按照图中所标注的数据计算图中实线所围成的图形的面积
______；
（3）类比探究：如图3，，
，将斜边
绕点逆时针旋转
至
，连接
，求
的面积．
（4）拓展提升：如图4，点，在
的边
、
上，点，
在内部的射线
上，
、
分别是
、
的外角．已知
，
．求证：
；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△ABD中，∠BAC=∠ABD=90°，点E为AD边上的一点，且AC=AE，连接CE交AB于点G，过点A作AF⊥AD交CE于点F.
(1)求证：△AGE≌△AFC；
(2)若AB=AC，求证：AD=AF+BD.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某零件如图所示,图纸要求∠A=90°，∠B=32°，∠C=21°，当检验员量得∠BDC=145°，就断定这个零件不合格,你能说出其中的道理吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
如图，在四边形 ABCD 中，已知∠ACB=∠BAD=105°，∠ABC=∠ADC=45°，
求证：CD=AB
小刚是这样思考的；由已知可得，∠CAB=30°，∠DAC=75°，∠DCA=60°，∠ACB+∠DAC=180°，由求证及特殊度数可联想到构造特殊三角形，即过点 A 作 AE⊥AB 交 BC 的延长线于点 E，对 AB=AE，∠E=∠D
在△ADC 与△CEA 中，
∠D = ∠E，∠DAC = ∠ECA = 75° ，AC = CA.
△ADC≌△CEA．
得 CD=AE=AB
请你参考小刚同学思考问题的方法，解决下面问题
如图，在四边形 ABCD 中，若∠ACB+∠CAD=180°，∠B=∠D，请问：CD 与 AB 否相等？若相等，请你给出证明；若不相等。请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
