
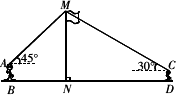
如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小明的眼睛与地面的距离(AB)是1.7 m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5 m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,结果保留整数).
≈1.7,结果保留整数).
|
分析:根据母题提供的思路,题目中出现了两个特殊角45°和30°,因此我们应该想方设法构造直角三角形,将这两个特殊角放在直角三角形中处理.不难想到应该过点A作AE⊥MN于点E,过点C作CF⊥MN于点F,虽然本题没有像母题那样出现一条公共的直角边,但直角边ME和MF之间相差0.2米,AE和CF的和为28米,可以设出未知数,找出两个相等关系,并根据一个相等关系设未知数,根据另一个相等关系列方程,因此本题可能有两种解法,从而求出ME和MF的长,继而求出旗杆MN的高度. 答:旗杆高约为12米. 解:如图,过点A作AE⊥MN于点E,过点C作CF⊥MN于点F,则EF=AB-CD=1.7-1.5=0.2.
在Rt△AEM中,∠AEM=90°,∠MAE=45°, 所以AE=ME. 设AE=ME=x,所以MF=x+0.2,CF=28-x. 在Rt△MFC中,∠MFC=90°,∠MCF=30°, 所以MF=CF·tan∠MCF,即x+0.2= 解得x≈10.0.所以MN≈12(米). 点评:这类问题中已知条件不一定告诉我们公共边的长度,也可能告诉的是其他线段的长,求公共边的长度. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据:
如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•高邮市二模)如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据:
(2012•高邮市二模)如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某数学兴趣小组进行测量学校旗杆高度的数学活动,甲、乙两人分别站在旗杆的东、西两侧相距80m的点A、B处,利用测角仪在标杆顶端D、E处侧得旗杆顶端C的仰角分别为30°、55°,测角仪距地面1.6m.求学校旗杆CF的高度(精确到0.1m)(参考数据sin55°≈0.81,cos55°≈0.57,tan55°≈1.42,
如图,某数学兴趣小组进行测量学校旗杆高度的数学活动,甲、乙两人分别站在旗杆的东、西两侧相距80m的点A、B处,利用测角仪在标杆顶端D、E处侧得旗杆顶端C的仰角分别为30°、55°,测角仪距地面1.6m.求学校旗杆CF的高度(精确到0.1m)(参考数据sin55°≈0.81,cos55°≈0.57,tan55°≈1.42,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:
如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30°.两人相距30米且位于旗杆两侧(点B,N,D在同一条直线上).求旗杆MN的高度.(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| 多边形的条数 | 4 | 5 | 6 | … | n |
| 连接线段的条数 | 1 | 2 | … | ||
| 分成三角形的个数 | 2 | 3 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com