
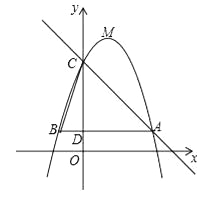
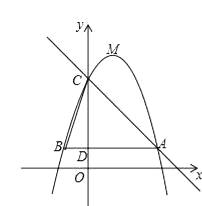
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(5,3),点C(0,8),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)求△ABC的面积;
(3)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
【答案】(1)y=﹣x2+4x+8,M(2,12);(2)15;(3)6<m<9.
【解析】试题分析:(1)把点A、C的坐标代入函数解析式,用待定系数法求出抛物线解析式;
(2)结合点A、B、C的坐标,三角形的面积公式进行解答;
(3)点M是沿着对称轴直线x=2向下平移的,可先求出直线AC的解析式,将x=2代入求出点M在向下平移时与AC、AB相交时y的值,即可得到m的取值范围.
解:(1)把点A(5,3),点C(0,8)代入二次函数y=﹣x2+bx+c,得
![]() ,
,
解得![]() ,
,
∴二次函数解析式为y=﹣x2+4x+8,配方得y=﹣(x﹣2)2+12
∴点M的坐标为(2,12);
(2)由(1)知,抛物线的对称轴是x=2.
∵A(5,3),AB∥x轴,
∴AB=6,D(0,3)
∵C(0,8),
∴CD=5,
∴△ABC的面积=![]() ABCD=
ABCD=![]() ×6×5=15,
×6×5=15,
即△ABC的面积=15;
(3)设直线AC解析式为y=kx+b,把点A(5,3),C(0,8)代入![]() ,
,
解得![]() ,
,
∴直线AC的解析式为y=﹣x+8,对称轴直线x=2与△ABC两边分别交于点E、点F,
把x=2代入直线AC解析式y=﹣x+8,
解得y=6,则点E坐标为(2,6),点F坐标为(2,3)
∴3<12﹣m<6,解得6<m<9.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=10 cm,BC=6 cm,动点P从点C出发,以每秒2 cm的速度按C→A的路径运动,设运动时间为t秒.
(1)出发2秒时,△ABP的面积为 cm2;
(2)当t为何值时,BP恰好平分∠ABC?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学使用计算器求30个数据的平均数时,错将其中一个数据108输入为18,那么由此求出的平均数与实际平均数的差是( )
A. 3.5 B. 3 C. 0.5 D. ﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
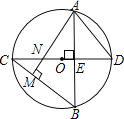
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
(3)若![]() 且AE=4,求CM
且AE=4,求CM
查看答案和解析>>
科目:初中数学 来源: 题型:
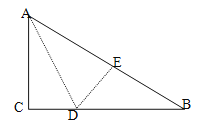
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示这个数字是( )
A.6.75×103吨
B.67.5×103吨
C.6.75×104吨
D.6.75×105吨
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com