
【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料,学校与图书馆的路程是![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线![]() 和线段
和线段![]() 分别表示两人离学校的路程
分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
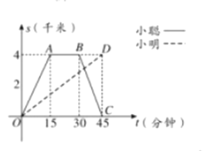
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)求线段![]() 的函数关系式;
的函数关系式;
(4)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
【答案】(1)15;![]() ;(2)s与t的函数关系式s=
;(2)s与t的函数关系式s=![]() t(0≤t≤45).(3)线段
t(0≤t≤45).(3)线段![]() 的函数解析式为s=-
的函数解析式为s=- ![]() t+12(30≤t≤45);(4)3千米
t+12(30≤t≤45);(4)3千米
【解析】
(1)直接根据图象上所给的数据的实际意义可求解;
(2)由图象可知,s是t的正比例函数,设所求函数的解析式为s=kt(k≠0),把(45,4)代入解析式利用待定系数法即可求解;
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设线段![]() 的函数解析式为s=mt+n(m≠0)把(30,4),(45,0)代入利用待定系数法先求得函数关系式,
的函数解析式为s=mt+n(m≠0)把(30,4),(45,0)代入利用待定系数法先求得函数关系式,
(4)根据求函数图象的交点方法求得函数交点坐标即可.
(1)∵3015=15,4÷15=![]()
∴小聪在天一阁查阅资料的时间和小聪返回学校的速度分别是15分钟,![]() 千米/分钟.
千米/分钟.
故答案为:15;![]() ;
;
(2)由图象可知,s是t的正比例函数
设所求函数的解析式为s=kt(k≠0)
代入(45,4),得
4=45k
解得k=![]()
∴s与t的函数关系式s=![]() t(0≤t≤45).
t(0≤t≤45).
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设线段![]() 的函数解析式为s=mt+n(m≠0)
的函数解析式为s=mt+n(m≠0)
代入(30,4),(45,0),得![]()
解得
∴s=- ![]() t+12(30≤t≤45),
t+12(30≤t≤45),
即线段![]() 的函数解析式为s=-
的函数解析式为s=- ![]() t+12(30≤tspan>≤45);
t+12(30≤tspan>≤45);
(4)令-![]() t+12=
t+12=![]() t,解得t=
t,解得t=![]()
当t=![]() 时,S=
时,S=![]() ×
×![]() =3.
=3.
答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
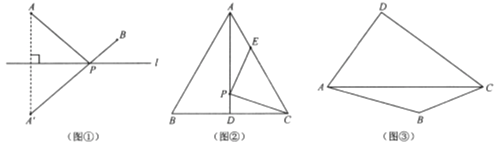
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=6,BC=8,若AC,BC边上的中线BE,AD 垂直相交于点O,则AB=( )

A. 5 B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
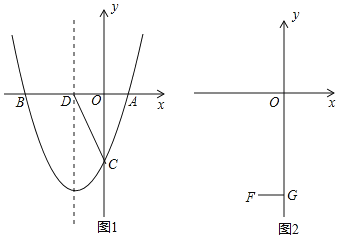
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
(1)若m=-3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在抛物线对称轴左侧上有 一点E,使S△ACE=S△ACD,求E点的坐标;
(3) 如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使 ∠OBP=∠FPG? 若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(﹣1,a),l1与y轴交于点C,l2与x轴交于点A.

(1)求a的值及直线l1的解析式.
(2)求四边形PAOC的面积.
(3)在x轴上方有一动直线平行于x轴,分别与l1,l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com