
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中:①ac>0;②a+b+c<0;③4a﹣2b+c<0;④2a+b<0;⑤4ac﹣b2<4a;⑥a+b>0中,其中正确的个数为( )
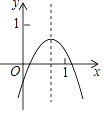
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线的顶点坐标情况进行推理,进而对所得结论进行判断.
①图象开口向下,与y轴交于负半轴,对称轴在y轴右侧,能得到:a<0,c<0,
∴ac>0,故①正确;
②当x=1时,y>0,∴a+b+c>0,故②错误;
③当x=-2时,y<0,∴4a-2b+c<0,故③正确;
④∵对称轴x=-![]() <1,
<1,
∴2a+b<0,故④正确;
⑤∵抛物线的顶点在x轴的上方,
∴![]() <1,
<1,
∵4a<0,
∴4ac-b2>4a,故⑤错误;
⑥∵2a+b>0,
∴2a+b-a>-a,
∴a+b>-a,
∵a<0,
∴-c>0,
∴a+b>0,故⑥正确;
综上所述正确的个数为4个,
故选C.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
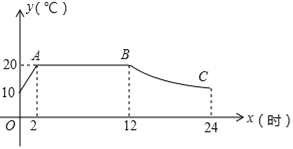
(1)求0到2小时期间y随x的函数解析式;
(2)恒温系统在一天内保持大棚内温度不低于15℃的时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
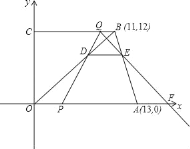
【题目】如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12).动点P、Q分别从O、B两点出发,点P以每秒2个单位的速度沿x轴向终点A运动,点Q以每秒1个单位的速度沿BC方向运动;当点P停止运动时,点Q也同时停止运动.线段PQ和OB相交于点D,过点D作DE∥x轴,交AB于点E,射线QE交x轴于点F.设动点P、Q运动时间为t(单位:秒).
(1)当t为何值时,四边形PABQ是平行四边形.
(2)△PQF的面积是否发生变化?若变化,请求出△PQF的面积s关于时间t的函数关系式;若不变,请求出△PQF的面积.
(3)随着P、Q两点的运动,△PQF的形状也随之发生了变化,试问何时会出现等腰△PQF?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,有下列结论:
①它的图象与x轴有两个交点;
②如果当x≤﹣1时,y随x的增大而减小,则m=﹣1;
③如果将它的图象向左平移3个单位后过原点,则m=1;
④如果当x=2时的函数值与x=8时的函数值相等,则m=5.
其中一定正确的结论是_______.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
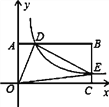
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=( )
A. 6 B. 9 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
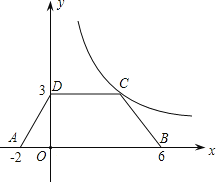
【题目】如图,等腰梯形ABCD放置在平面坐标系中,已知A(﹣2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
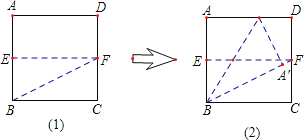
【题目】折纸与证明﹣﹣﹣用纸折出黄金分割点:
第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com