
如图,△ABC是等腰直角三角形,∠A=90°,点P,Q分别是AB, AC上的一动点,且满足BP=AQ,D是
AC上的一动点,且满足BP=AQ,D是 BC的中点.
BC的中点.
(1)求证:△PDQ是等腰直角三角形.
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( )
A.8,8 B.8.4,8 C.8.4,8.4 D.8,8.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC的周长是32,以它的三边中点为顶点组成第2个三角形,再以第2个三角形的三边中点为顶点组成第3个三角形,…,则第n个三角形的周长为 .
 ‘
‘
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,平行四边形ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点M,N,若△CON的面积为2,△DOM的面积为4,则△AOB的面积为 .
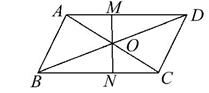
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2 B.3 C.2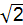 D.2
D.2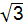
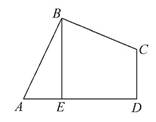
查看答案和解析>>
科目:初中数学 来源: 题型:
小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件:如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元.按此优惠条件,小丽一次性购买这种服装付了1200元.请问她购买了多少件这种服装?(8分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com