
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.
(1)求点D的坐标;
(2)如图(1),求△ACD的面积;
(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.
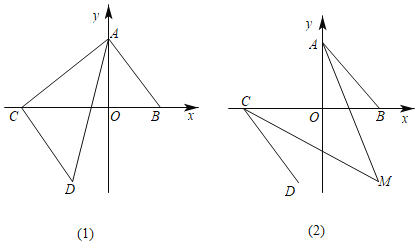
【答案】(1)D(﹣2,﹣4);(2)16;(3)∠M=45°,理由见解析
【解析】
(1)根据平移规律可得点D的坐标;
(2)利用面积差可得结论;
(3)先根据直角三角形的两锐角互余得:∠OAB+∠ABO=90°,由角平分线定义得:∠MCB+∠OAM=![]() (∠DCB+∠OAB)=45°,最后根据三角形的内角和可得结论.
(∠DCB+∠OAB)=45°,最后根据三角形的内角和可得结论.
解:(1)∵ B(3,0),
∴ OB=3,
∵ BC=8,
∴ OC=5,
∴ C(﹣5,0),
∵ AB∥CD,AB=CD,
∴ D(﹣2,﹣4);
(2)如图(1),连接OD,
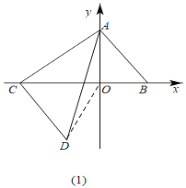
∴S△ACD=S△ACO+S△DCO﹣S△AOD=![]() ﹣
﹣![]() =16;
=16;
(3)∠M=45°,理由是:
如图(2),连接AC,
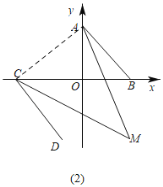
∵AB∥CD,
∴∠DCB=∠ABO,
∵∠AOB=90°,
∴∠OAB+∠ABO=90°,
∴∠OAB+∠DCB=90°,
∵∠OAB与∠OCD的角平分线相交于点M,
∴∠MCB=![]() ,∠OAM=
,∠OAM=![]() ,
,
∴∠MCB+∠OAM=![]() =45°,
=45°,
△ACO中,∠AOC=∠ACO+∠OAC=90°,
△ACM中,∠M+∠ACM+∠CAM=180°,
∴∠M+∠MCB+∠ACO+∠OAC+∠OAM=180°,
∴∠M=180°﹣90°﹣45°=45°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
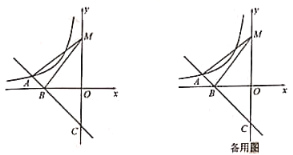
【题目】如图,平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 在第二象限内的图像相交于点A,与
在第二象限内的图像相交于点A,与![]() 轴的负半轴交于点B,与
轴的负半轴交于点B,与![]() 轴的负半轴交于点C.
轴的负半轴交于点C.
(1)求∠BCO的度数;
(2)若![]() 轴上一点M的纵坐标是4,且B点坐标为(-3,0),求AM的长.
轴上一点M的纵坐标是4,且B点坐标为(-3,0),求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意一点
中,对于任意一点![]() ,定义点
,定义点![]() 的“离心值”
的“离心值”![]() 为:
为: 时,例如对于点
时,例如对于点![]() ,因为
,因为![]() ,所以
,所以![]() .
.
解决下列问题:
(1)已知![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值,并将
的值,并将![]() ,
,![]() ,
,![]() 按从小到大的顺序排列(用“<”连接);
按从小到大的顺序排列(用“<”连接);
(2)如图,点![]() ,线段
,线段![]() 上的点
上的点![]() ,
,
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②在图中画出满足![]() 的点
的点![]() 组成的图形,并用语言描述该图形的特征;
组成的图形,并用语言描述该图形的特征;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,D,C,且相互平行,若l1,l2的距离为2,l2,l3的距离为4,则正方形的对角线长为_______________.
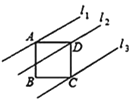
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
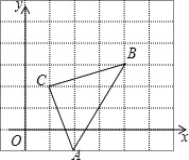
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ 、 )
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形![]() 中,
中,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 的速度移动,如果点
的速度移动,如果点![]() 同时出发,用
同时出发,用![]() 表示移动的时间(
表示移动的时间(![]() ).
).
(1)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(2)求四边形![]() 的面积,并探索一个与计算结果有关的结论.
的面积,并探索一个与计算结果有关的结论.
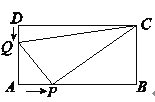
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,其中点
两点,其中点![]() ,点
,点![]() ,点
,点![]() 都在抛物线上,M为抛物线的顶点.
都在抛物线上,M为抛物线的顶点.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
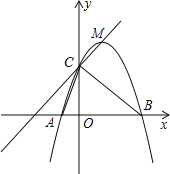
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com