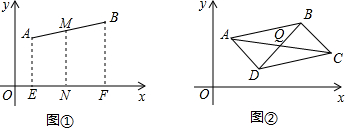
让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.
第一步:数轴上两点连线的中点表示的数.自己画一个数轴,如果点A、B分别表示-2、4,则线段AB的中点M表示的数是
1
1
. 再试几个,我们发现:数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数.
第二步;平面直角坐标系中两点连线的中点的坐标(如图①)为便于探索,我们在第一象限内取两点A(x
1,y
1),B(x
2,y
2),取线段AB的中点M,分别作A、B到x轴的垂线段AE、BF,取EF的中点N,则MN是梯形AEFB的中位线,故MN⊥x轴,利用第一步的结论及梯形中位线的性质,我们可以得到点M的坐标是(
,
)(用x
1,y
1,x
2,y
2表示),AEFB是矩形时也可以.我们的结论是:平面直角坐标系中连接两点的线段的中点的横(纵)坐标等于这两点的横(纵)坐标的平均数.
第三步:平面直角坐标系中平行四边形的顶点坐标之间的关系(如图②)在平面直角坐标系中画一个平行四边形ABCD,设A(x
1,y
1),B(x
2,y
2),C(x
3,y
3),D(x
4,y
4),则其对角线交点Q的坐标可以表示为Q(
,
),也可以表示为Q(
,
),经过比较,我们可以分别得出关于x
1,x
2,x
3,x
4及,y
1,y
2,y
3,y
4的两个等式是
x1+x3=x2+x4
x1+x3=x2+x4
和
y1+y3=y2+y4
y1+y3=y2+y4
. 我们的结论是:平面直角坐标系中平行四边形的对角顶点的横(纵)坐标的
和相等
和相等
.

 图象上的任意两点,且y1<y2,则x1,x2可能满足的关系是( )
图象上的任意两点,且y1<y2,则x1,x2可能满足的关系是( )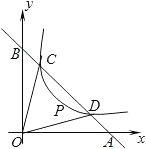 y1)、D(x2,y2),连接OC、OD(O是坐标有点),若∠BOC=∠AOD=α,且tanα=
y1)、D(x2,y2),连接OC、OD(O是坐标有点),若∠BOC=∠AOD=α,且tanα=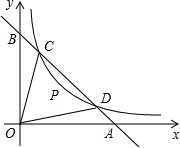 ,D(x2,y2),连接OC,OD(O是坐标原点),若∠BOC=∠AOD=α,且tanα=
,D(x2,y2),连接OC,OD(O是坐标原点),若∠BOC=∠AOD=α,且tanα=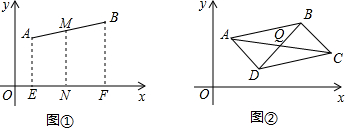 让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.
让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系.