
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题: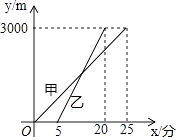
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
【答案】
(1)解:由图可得,起点A与终点B之间相距3000米;
(2)解:由图可得,甲龙舟队先出发,乙龙舟队先到达终点;
(3)解:设甲龙舟队的y与x函数关系式为y=kx,
把(25,3000)代入,可得3000=25k,
解得k=120,
∴甲龙舟队的y与x函数关系式为y=120x(0≤x≤25),
设乙龙舟队的y与x函数关系式为y=ax+b,
把(5,0),(20,3000)代入,可得
![]() ,
,
解得 ![]() ,
,
∴乙龙舟队的y与x函数关系式为y=200x﹣1000(5≤x≤20);
(4)解:令120x=200x﹣1000,可得x=12.5,
即当x=12.5时,两龙舟队相遇,
当x<5时,令120x=200,则x= ![]() (符合题意);
(符合题意);
当5≤x<12.5时,令120x﹣(200x﹣1000)=200,则x=10(符合题意);
当12.5<x≤20时,令200x﹣1000﹣120x=200,则x=15(符合题意);
当20<x≤25时,令3000﹣120x=200,则x= ![]() (符合题意);
(符合题意);
综上所述,甲龙舟队出发 ![]() 或10或15或
或10或15或 ![]() 分钟时,两支龙舟队相距200米
分钟时,两支龙舟队相距200米
【解析】(1)由已知条件利用函数图象即可求出两点距离;
(2)根据函数图象即可得出所求结论;
(3)先设甲龙舟队的y与x函数关系式为y=kx,把(25,3000)代入,可得甲龙舟队的y与x函数关系式;再设乙龙舟队的y与x函数关系式为y=ax+b,把(5,0),(20,3000)代入,可得乙龙舟队的y与x函数关系式;
(4)根据题意分四种情况进行讨论,由已知条件分别列方程求解即可得到结论.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.

(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OM⊥ON,斜边长为4的等腰直角△ABC的斜边AC在射线上,顶点C与O重合,若点A沿NO方向向O运动,△ABC的顶点C随之沿OM方向运动,点A移动到点O为止,则直角顶点B运动的路径长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动问题情境:
如图1,在△ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将△ADE绕点A顺时针旋转α角(0°<α<90°)得到△AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
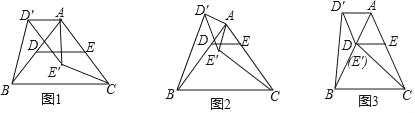
探究发展:
(1)图1中,猜想CE′与BD′的数量关系,并证明;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E“,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在△ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将△ADE绕点A顺时针旋转60°得到△AD′E′,连接CE′,BD′,请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1,2,3,……,100这100个自然数,任意分为50组,每组两个数,现将每组的两个数中任一数值记作a,另一个记作b,代入代数式![]() 中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是___________
中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ![]() ,﹣2);⑤当x<
,﹣2);⑤当x< ![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )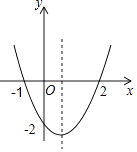
A.3个
B.4个
C.5个
D.6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为 . 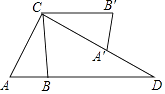
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
(1)试证明:DE=BF;
(2)连接DF,BE,猜想DF与BE的关系?并证明你的猜想的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com