
 某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.
某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.分析 (1)①根据函数图象,即可解答;
②设y1=k1x+b,把(0,40),(30,0)代入得到方程组即可;设y2=k2x,把(120,40)代入即可解答;
③联立y1,y2得到方程组,求出方程组的解,即可求出M点的坐标;
(2)结合函数图象,提出问题即可.
解答 解:(1)①根据图象得:A,B两个码头之间的距离是40千米;故答案为:40;
②设y1=k1x+b,
把(0,40),(30,0)代入得:$\left\{\begin{array}{l}{b=40}\\{30{k}_{1}+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-\frac{4}{3}}\\{b=40}\end{array}\right.$,
∴${y}_{1}=-\frac{4}{3}x+40$,
设y2=k2x,
把(120,40)代入得:40=120k2,
解得:${k}_{2}=\frac{1}{3}$,
∴${y}_{2}=\frac{1}{3}x$;
③联立${y}_{1}=-\frac{4}{3}x+40$与${y}_{2}=\frac{1}{3}x$得:$\left\{\begin{array}{l}{y=-\frac{4}{3}x+40}\\{y=\frac{1}{3}x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=24}\\{y=8}\end{array}\right.$,
∴点M的坐标为(24,8),
它的实际意义是:两船同时出发经24分钟相遇,此时距B码头8千米.
故答案为:(24,8),两船同时出发经24分钟相遇,此时距B码头8千米.
(2)货轮比客轮晚几分钟到达目的地?
点评 本题考查了一次函数的应用,解决本题的关键是用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.


科目:初中数学 来源: 题型:选择题
| A. | 9.001×10-3 | B. | -9.001×10-3 | C. | 0.9001×10-3 | D. | -0.9001×10-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
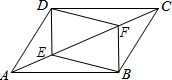 已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com