
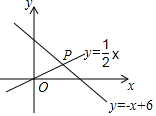 (1)计算(2$\sqrt{3}$-1)2
(1)计算(2$\sqrt{3}$-1)2分析 (1)根据完全平方公式进行展开,即可得出结果;
(2)运算顺序:先乘方再乘除,最后加减,有括号的先算括号里面的;
(3)运用加减消元法进行求解,即可得到方程组的解;
(4)由两个一次函数表达式组成的方程组的解就是两条直线的交点的坐标.
解答 解:(1)(2$\sqrt{3}$-1)2
=(2$\sqrt{3}$)2-2×2$\sqrt{3}$×1+12
=12+4$\sqrt{3}$+1
=13-4$\sqrt{3}$;
(2)($\sqrt{6}$-2$\sqrt{15}$)×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$
=$\sqrt{18}$-2$\sqrt{45}$-6×$\frac{\sqrt{2}}{2}$
=3$\sqrt{2}$-2×3$\sqrt{5}$-3$\sqrt{2}$
=-6$\sqrt{5}$;
(3)$\left\{\begin{array}{l}{x+y=300①}\\{2x+5y=1140②}\end{array}\right.$
由②-①×2,得
3y=540,
解得y=180,
把y=180代入①,得
x+180=300,
解得x=120,
∴方程组的解为$\left\{\begin{array}{l}{x=120}\\{y=180}\end{array}\right.$;
(4)解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=-x+6}\end{array}\right.$,可得
$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,
∴交点P的坐标为(4,2).
点评 本题主要考查了二次根式的运算、解二元一次方程组以及求一次函数图象交点的坐标,解题时注意:方程组的两个方程中,如果同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数,再把两个方程的两边分别相减或相加,即可消去一个未知数.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
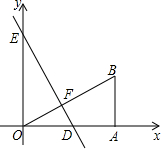 如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,交OB于点F.
如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,交OB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
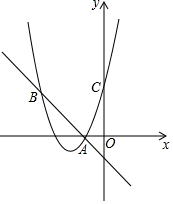 如图,已知二次函数y1=ax2+bx+c的图象经过点A(-1,0),C(0,3),且对称轴为直线x=-2,一次函数y2=mx+n的图象经过点A、B.
如图,已知二次函数y1=ax2+bx+c的图象经过点A(-1,0),C(0,3),且对称轴为直线x=-2,一次函数y2=mx+n的图象经过点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四点A、B、C、D,按照下列语句画出图形;
如图,四点A、B、C、D,按照下列语句画出图形;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com