
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE.
(1)求证:∠B=∠D;
(2)若AB=13,BC﹣AC=7,求CE的长.
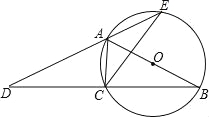
【答案】(1)证明见试题解析;(2)CE=12.
【解析】
试题分析:(1)由AB为⊙O的直径,易证得AC⊥BD,又由DC=CB,根据线段垂直平分线的性质,可证得AD=AB,即可得:∠B=∠D;
(2)首先设BC=x,则AC=x﹣7,由在Rt△ABC中,AC2+BC2=AB2,可得方程:(x﹣7)2+x2=132,解此方程即可求得CB的长,继而求得CE的长.
试题解析:(1)∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,
又∵DC=CB,∴AD=AB,∴∠B=∠D;
(2)设BC=x,则AC=x﹣7,在Rt△ABC中,AC2+BC2=AB2,即(x﹣7)2+x2=132,
解得:x1=12,x2=﹣5(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,
∵CD=CB,∴CE=CB=12.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
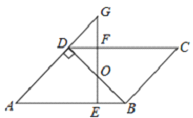
【题目】如图,四边形ABCD中,DC∥AB ,BD⊥AD,∠A=45°,E、F分别是AB、CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=2时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程-x2+3x=1用公式法求解,先确定a , b , c的值,正确的是( )
A.a=-1,b=3,c=-1
B.a=-1,b=3,c=1
C.a=-1,b=-3,c=-1
D.a=1,b=-3,c=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.如果汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,那么汽车在乡村公路上的行驶速度为km/h. 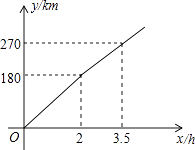
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积. 例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2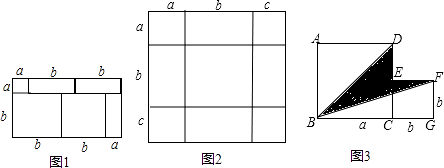
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com