
【题目】如图,方格纸中每个小方格都是边长为1的正方形,已知学校的坐标为A(2,2).
(1)请在图中建立适当的直角坐标系,并写出图书馆的坐标;
(2)若体育馆的坐标为C(-2,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB= ![]() BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.
BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG. 
(1)判断四边形EFDG的形状,并证明;
(2)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明. 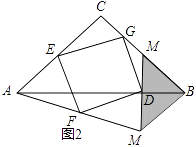
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长. 例如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D,若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B,…设游戏者从圈A起跳.
(1)若随机掷一次骰子,求落回到圈A的概率P1;
(2)若随机掷两次骰子,用列表法或树状图法求出最后落回到圈A的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN. 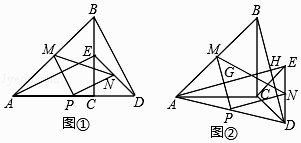
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
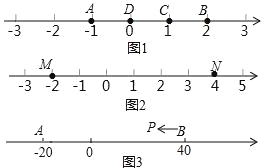
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y= ![]() 的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0). 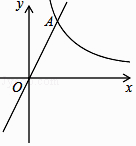
(1)求平移后直线的表达式;
(2)求OA平移后所得直线与双曲线的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点.若∠A=60°,则∠BMN的度数为( )

A. 45° B. 50° C. 60° D. 65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com