
【题目】如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为![]() 的中点,过点D作DE∥AC,交BC的延长线于点E.
的中点,过点D作DE∥AC,交BC的延长线于点E.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若CE=![]() ,AB=6,求⊙O的半径.
,AB=6,求⊙O的半径.
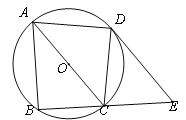
【答案】(1)DE与⊙O相切;理由见解析;(2)4.
【解析】
(1)连接OD,由D为![]() 的中点,得到
的中点,得到![]() ,进而得到AD=CD,根据平行线的性质得到∠DOA=∠ODE=90°,求得OD⊥DE,于是得到结论;
,进而得到AD=CD,根据平行线的性质得到∠DOA=∠ODE=90°,求得OD⊥DE,于是得到结论;
(2)连接BD,根据四边形对角互补得到∠DAB=∠DCE,由![]() 得到∠DAC=∠DCA=45°,求得△ABD∽△CDE,根据相似三角形的性质即可得到结论.
得到∠DAC=∠DCA=45°,求得△ABD∽△CDE,根据相似三角形的性质即可得到结论.
(1)解:DE与⊙O相切
证:连接OD,在⊙O中
∵D为![]() 的中点
的中点
∴![]()
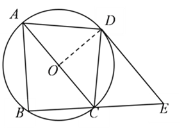
∴AD=DC
∵AD=DC,点O是AC的中点
∴OD⊥AC
∴∠DOA=∠DOC=90°
∵DE∥AC
∴∠DOA=∠ODE=90°
∵∠ODE=90°
∴OD⊥DE
∵OD⊥DE,DE经过半径OD的外端点D
∴DE与⊙O相切.
(2)解:连接BD
∵四边形ABCD是⊙O的内接四边形
∴∠DAB+∠DCB=180°
又∵∠DCE+∠DCB=180°
∴∠DAB=∠DCE
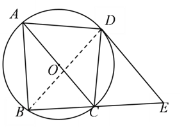
∵AC为⊙O的直径,点D、B在⊙O上,
∴∠ADC=∠ABC=90°
∵![]() ,
,
∴∠ABD=∠CBD=45°
∵AD=DC,∠ADC=90°
∴∠DAC=∠DCA=45°
∵DE∥AC
∴∠DCA=∠CDE=45°
在△ABD和△CDE中
∵∠DAB=∠DCE,∠ABD=∠CDE=45°
∴△ABD∽△CDE
∴![]() =
=![]()
∴![]() =
=![]()
∴AD=DC=4![]() , CE=
, CE=![]() ,AB=6,
,AB=6,
在Rt△ADC中,∠ADC=90°,AD=DC=4![]() ,
,
∴AC=![]() =8
=8
∴⊙O的半径为4.



科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线相交于点O,且点O是BD的中点,若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )

A.40B.24C.20D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+bx+c(b,c为常数)的图象经过点(2,3),(3,0).
(1)则b=,c=;
(2)该二次函数图象与y轴的交点坐标为,顶点坐标为;
(3)在所给坐标系中画出该二次函数的图象;
(4)根据图象,当-3<x<2时,y的取值范围是.
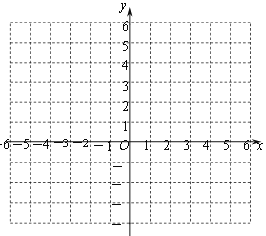
查看答案和解析>>
科目:初中数学 来源: 题型:
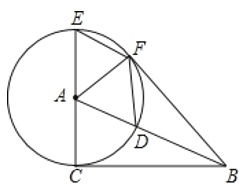
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当四边形![]() 是周长为20的菱形时,
是周长为20的菱形时,![]() ;
;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
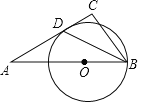
【题目】如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2![]() ,则线段CD的长是( )
,则线段CD的长是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
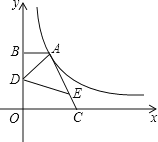
【题目】如图,点A在双曲线y=![]() 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为
的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为![]() ,则k的值为______.
,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
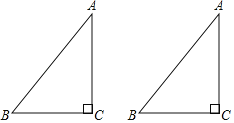
【题目】下面是小宇设计的“作已知直角三角形的中位线”的尺规作图过程.
已知:在△ABC中,∠C=90°.
求作:△ABC的中位线DE,使点D在AB上,点E在AC上.
作法:如图,
①分别以A,C为圆心,大于![]() AC长为半径画弧,两弧交于P,Q两点;
AC长为半径画弧,两弧交于P,Q两点;
②作直线PQ,与AB交于点D,与AC交于点E.
所以线段DE就是所求作的中位线.
根据小宇设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接PA,PC,QA,QC,DC,
∵PA=PC,QA= ,
∴PQ是AC的垂直平分线( )(填推理的依据).
∴E为AC中点,AD=DC.
∴∠DAC=∠DCA,
又在Rt△ABC中,有∠BAC+∠ABC=90°,∠DCA+∠DCB=90°.
∴∠ABC=∠DCB( )(填推理的依据).
∴DB=DC.
∴AD=BD=DC.
∴D为AB中点.
∴DE是△ABC的中位线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com