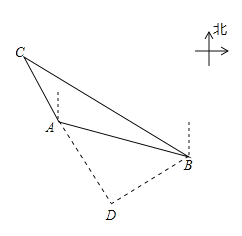
【题目】如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°向的C地，有一艘渔船遇险，要求马上前去救援．此时C地位于北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之间的距离为16海里．求A、C两地之间的距离．（保留根号）
【答案】
．
【解析】
试题过点B作BD⊥CA交CA延长线于点D，根据题意可得∠ACB和∠ABC的度数，然后根据三角形外角定理求出∠DAB的度数，已知AB=12海里，可求出BD、AD的长度，在Rt△CBD中，解直角三角形求出CD的长度，继而可求出A、C之间的距离．
试题解析：解：过点B作BD⊥CA交CA延长线于点D， 由题意得，∠ACB=60°﹣30°=30°，∠ABC=75°﹣60°=15°，∴∠DAB=∠DBA=45°，在Rt△ABD中，AB=16海里，∠DAB=45°，∴BD=AD=ABcos45°=
（海里），在Rt△CBD中，CD=
=
，∴AC=（
）（海里）．
答：A、C两地之间的距离是海里．
新题型全程检测期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数为（ ）
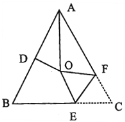
A.120°B.108°C.110°D.102°
查看答案和解析>>
科目：初中数学 来源： 题型：
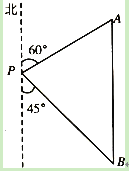
【题目】五一期间，小红到美丽的世界地质公园湖光岩参加社会实践活动，在景点P处测得景点B位于南偏东45°方向；然后沿北偏东60°方向走100米到达景点A，此时测得景点B正好位于景点A的正南方向，求景点A与B之间的距离．（结果精确到0.1米）
查看答案和解析>>
科目：初中数学 来源： 题型：
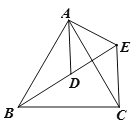
【题目】如图，△ ABC 和△ADE都是等边三角形，点 B 在 ED 的延长线上．
（1）求证：△ABD≌△ACE．
（2）求证：AE＋CE=BE．
（3）求∠BEC 的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
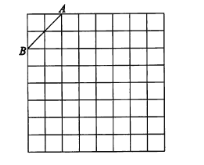
【题目】如图，是规格为8×8的正方形网格，请在所给网格中按下列要求操作：
(1)在网格中建立平面直角坐标系，使A点坐标为(-2，4)，B点坐标为(-4，2)；
(2)在(1)的前提下，在第二象限内的格点上找一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点的坐标是；
(3)求((2)中△ABC的周长(结果保留根号)；
(4)画出((2)中△ABC关于y轴对称的△A'B'C'.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝x＋3与坐标轴分别交于A，B两点，抛物线y＝ax2＋bx－3a经过点A，B，顶点为C，连接CB并延长交x轴于点E，点D与点B关于抛物线的对称轴MN对称．
（1）求抛物线的解析式及顶点C的坐标；
（2）求证：四边形ABCD是直角梯形．
【答案】（1）y＝－x2－2x＋3，顶点C的坐标为（－1，4）；（2）证明见解析．
【解析】
（1）解：∵y＝x＋3与坐标轴分别交与A，B两点，∴A点坐标（－3，0）、B点坐标（0，3）.
∵抛物线y＝ax2＋bx－3a经过A，B两点，
∴
解得
∴抛物线解析式为：y＝－x2－2x＋3.
∵y＝－x2－2x＋3＝－（x＋1）2＋4，
∴顶点C的坐标为（－1，4）.
（2）证明：∵B，D关于MN对称，C（－1，4），B（0，3），
∴D（－2，3）.∵B（0，3），A（－3，0），∴OA＝OB.
又∠AOB＝90°，∴∠ABO＝∠BAO＝45°.
∵B，D关于MN对称，∴BD⊥MN.
又∵MN⊥x轴，∴BD∥x轴.
∴∠DBA＝∠BAO＝45°.
∴∠DBO＝∠DBA＋∠ABO＝45°＋45°＝90°.
设直线BC的解析式为y＝kx＋b，
把B（0，3），C（－1，4）代入得，
解得
∴y＝－x＋3.
当y＝0时，－x＋3＝0，x＝3，∴E（3，0）.
∴OB＝OE，又∵∠BOE＝90°，
∴∠OEB＝∠OBE＝∠BAO＝45°.
∴∠ABE＝180°－∠BAE－∠BEA＝90°.
∴∠ABC＝180°－∠ABE＝90°.
∴∠CBD＝∠ABC－∠ABD＝45°.
∵CM⊥BD，∴∠MCB＝45°.
∵B，D关于MN对称，
∴∠CDM＝∠CBD＝45°，CD∥AB.
又∵AD与BC不平行，∴四边形ABCD是梯形.
∵∠ABC＝90°，∴四边形ABCD是直角梯形.
【题型】解答题
【结束】
21
【题目】有两组卡片，第一组三张卡片上都写着A、B、B，第二组五张卡片上都写着A、B、B、D、E．试用列表法求出从每组卡片中各抽取一张，两张都是B的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
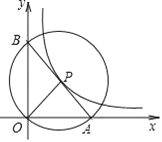
【题目】如图，在平面直角坐标系中，O 为坐标原点，P是反比例函数
图象上任意一点，以P为圆心，PO为半径的圆与x轴交于点 A、与y轴交于点B，连接AB．
（1）求证：P为线段AB的中点；
（2）求△AOB的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
