
【题目】广州中学在“读书日”期间购进一批图书, 需要用大小两种规格的纸箱来装运.![]() 个大纸箱和
个大纸箱和![]() 个小纸箱一次可以装
个小纸箱一次可以装![]() ,本书
,本书![]() 个大纸箱和
个大纸箱和![]() 个小纸箱--次可以装
个小纸箱--次可以装![]() 本书.
本书.
(1)一个大纸箱和一个小纸箱分别可以装多少本书?
(2)如果一共购入![]() 本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
【答案】(1)一个大纸箱可以装30本书,一个小纸箱可以装20本书;(2)共有2种装书方案.用5个小纸箱;用2个大纸箱,2个小纸箱.
【解析】
(1)设一个大纸箱可以装x本书,一个小纸箱分别可以装y本书,根据1个大纸箱和1个小纸箱一次可以装50本书,2个大纸箱和3个小纸箱一次可以装120本书列方程组求解即可;
(2)设需m个大纸箱,n个小纸箱,根据一共购入100本书列二元一次方程求解即可.
(1)设一个大纸箱可以装x本书,一个小纸箱可以装y本书·依题意,
得:![]()
解得![]() ·
·
答:一个大纸箱可以装30本书,一个小纸箱可以装20本书.
(2)设需要用m个大纸箱,n个小纸箱,
依题意,得:30m+20n=100.
∵m,n均为正整数,
∴共有2种装书方案.用5个小纸箱不用大纸箱或用2个大纸箱,2个小纸箱.


科目:初中数学 来源: 题型:
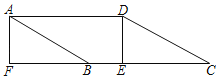
【题目】如图,在ABCD中,∠C=30°,过D作DE⊥BC于点E,延长CB至点F,使BF=CE,连接AF.若AF=4,CF=10![]() ,则ABCD的面积为_____.
,则ABCD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以8m/s的速度行驶,从不同出口驶出,其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示,结合题目信息,下列说法错误的是( )
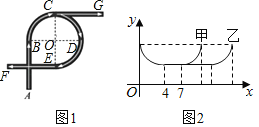
A.立交桥总长为168 m
B.从F口出比从G口出多行驶48m
C.甲车在立交桥上共行驶11 s
D.甲车从F口出,乙车从G口出
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() .
.
(1)确定二次函数![]() 的解析式;
的解析式;
(2)如图1,![]() 时,
时,![]() 交二次函数
交二次函数![]() 的图象于点
的图象于点![]() 的面积记作
的面积记作![]() 为何值时
为何值时![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
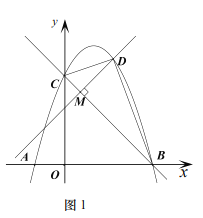
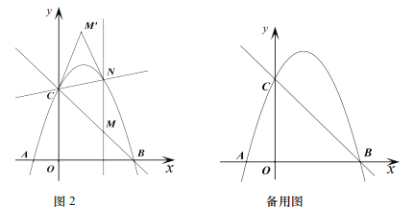
(3)如图2,过点![]() 作
作![]() 轴的平行线交二次函数
轴的平行线交二次函数![]() 的图象于点
的图象于点![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称是否存在点
对称是否存在点![]() 使四边形
使四边形![]() 为菱形,若存在直接写出
为菱形,若存在直接写出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
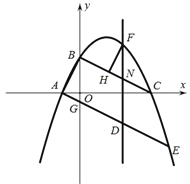
【题目】如图所示,在平面直角坐标系中,抛物线![]() 与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点
与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点![]() 为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
(1)求抛物线的表达式及直线BC的表达式;
(2)在点D运动的过程中,当FN的值最大时,在线段BC上是否存在一点H,使得FNH与ABC相似,如果存在,求出此时H点的坐标;
(3)当DF=4时,连接DC,四边形ABCD先向上平移一定单位长度后,使点D落在x轴上,然后沿x轴向左平移n(1n4)个单位长度,用含n的表达式表示平移后的四边形与原四边形重叠部分的面积S(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,某单位计划选购甲,乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.求甲,乙两种物品的单价各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的疫情防控意识,响应“停课不停学”号召,某校组织了一次“疫情防控知识”专题网上学习,并进行了一次全校2500名学生都参加的网上测试.阅卷后,教务处随机抽取了100份答卷进行分析统计,发现考试成绩(![]() 分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分)的最低分为51分,最高分为满分100分,并绘制了如下不完整的统计图表.请根据图表提供的信息,解答下列问题:
分数段(分) | 频数(人) | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |

(1)填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)将频数分布直方图补充完整;
(3)该校对成绩为![]() 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为
的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为![]() ,请你估算全校获得二等奖的学生人数;
,请你估算全校获得二等奖的学生人数;
(4)结合调查的情况,为了提高疫情防控意识,请你给学校提一条合理性建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com