
分析 (1)列举出所有情况,看足球踢到了丙处的情况数占所有情况数的多少即可;
(2)可设球从甲小明处先开始踢,得到3次踢球回到甲处的概率,进而根据树状图可得球从其他2位同学处开始,3次踢球回到甲处的概率,比较可得可能性最小的方案.
解答 解:(1)如图: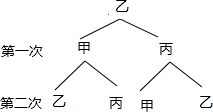
∴P(足球踢到丙处)=$\frac{1}{4}$;
(2)应从甲开始踢如图: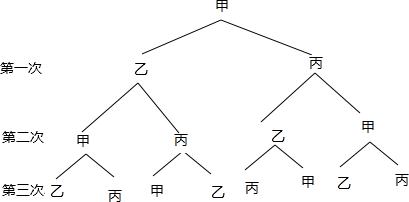
若从甲开始踢,P(踢到甲处)=$\frac{2}{8}$=$\frac{1}{4}$;
同理,若从乙开始踢,P(踢到乙处)=$\frac{3}{8}$;
若从丙开始踢,P(踢到丙处)=$\frac{3}{8}$.
点评 考查用列树状图的方法解决概率问题;分类得到3次踢球踢到甲处的情况数是解决本题的难点;用到的知识点为:概率等于所求情况数与总情况数之比.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:解答题
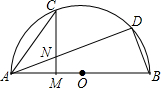 如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.
如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B是x轴上的两点,C在y轴上,且BO=CO=6cm,点A(4,0).
如图,A,B是x轴上的两点,C在y轴上,且BO=CO=6cm,点A(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在锐角△ABC中,高线CD、BE相交于点F,若∠A=55°,则∠BFC的度数是( )
如图,在锐角△ABC中,高线CD、BE相交于点F,若∠A=55°,则∠BFC的度数是( )| A. | 110° | B. | 125° | C. | 135° | D. | 145° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,2) | B. | (-2,4) | C. | (-4,2) | D. | (2,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com