
| A. | $\sqrt{{2^2}+{7^2}}$=2+7 | B. | $\sqrt{9\frac{1}{2}}$=3$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\frac{{\sqrt{8}+\sqrt{12}}}{{\sqrt{2}}}$=4+6 |
分析 根据最简二次根式的定义对A、B进行判断;根据二次根式的除法法则对C、D进行判断.
解答 解:A、原式=$\sqrt{4+49}$=$\sqrt{53}$,所以A选项的计算错误;
B、原式=$\sqrt{\frac{19}{2}}$=$\frac{\sqrt{38}}{2}$,所以B选项的计算错误;
C、原式=$\sqrt{6÷3}$=$\sqrt{2}$,所以C选项的计算正确;
D、原式=$\sqrt{8÷2}$+$\sqrt{12÷2}$=2+$\sqrt{6}$,所以D选项的计算错误.
故选C.
点评 本题考查了二次根式的混合计算:先把二次根式化为最简二次根式,然后进行二次根式的运算,最后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | 5$\sqrt{6}$-3$\sqrt{3}$=2$\sqrt{3}$ | C. | ($\sqrt{8}$+$\sqrt{50}$)÷2=$\sqrt{4}$+$\sqrt{25}$=7 | D. | 3$\sqrt{3}$+$\sqrt{27}$=6$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
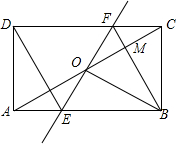 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=3:2.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点A(1,6),B(3,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
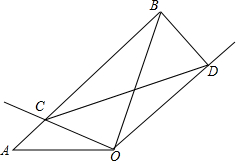 如图,在△AOB中,∠AOB=α,点C是边AB上与A、B不重合的一点,将射线OC绕点O顺时针旋转一定角度,旋转角等于α,得射线ON,以C为顶点,CO为一边作∠OCD=∠A.射线CD交ON于点D,连接BD.
如图,在△AOB中,∠AOB=α,点C是边AB上与A、B不重合的一点,将射线OC绕点O顺时针旋转一定角度,旋转角等于α,得射线ON,以C为顶点,CO为一边作∠OCD=∠A.射线CD交ON于点D,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com