【题目】如图：∠EAF=15°，AB=BC=CD=DE=EF，则∠DEF等于（ ）
A.60°B.75°C.70°D.90°
【答案】A
【解析】
根据已知条件，利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算．
∵AB=BC=CD=DE=EF
∠A=15°
∴∠BCA=∠A=15°
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°
∴∠BCD=180°(∠CBD+∠BDC)=180°60°=120°
∴∠ECD=∠CED=180°∠BCD∠BCA=180°120°15°=45°
∴∠CDE=180°(∠ECD+∠CED)=180°90°=90°
∴∠EDF=∠EFD=180°∠CDE∠BDC=180°90°30°=60°
∴∠DEF=180°(∠EDF+∠EFC)=180°120°=60°
故选A.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】已知如图，在 ABC 中，BAC 90° ,分别过顶点 B、C 作 A 点的直线的垂线垂足分别为 D、E,试探究线段 BD、CE、DE 之间的关系.
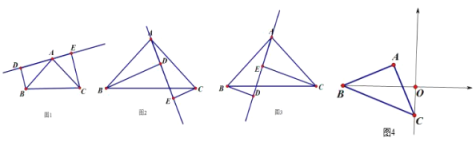
(1)当直线 DE 绕点 A 旋转至如图 1 的位置，直接写出 BD、CE、DE 之间的数量 为 ；
(2)当直线 DE 绕点 A 旋转至如图 2 的位置，直接写出 BD、CE、DE 之间的数量 为 ；
(3)当直线 DE 绕点 A 旋转至如图 3 的位置，写出 BD、CE、DE 之间的数量，并证明 你的结论；
(4)如图 4，如果将 ABC 放在直角坐标系中，若点 A 的坐标为(-1,1),求 OB-OC 的 值.请写出必要的解答步骤.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等腰△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段BC上，如果∠BAC=90°，求∠BCE的度数；
（2）如图2，当点D在线段BC上，如果∠BAC=60°，则∠BCE的度数；
（3）设∠BAC=α，∠BCE=β，如图3，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为 度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点D，E，F分别是△ABC的边AB，AC，BC上的点，DE∥BC，DF∥AC．
（1）如图1，点G是线段FD延长线上一点，连接EG，∠CEG的平分线EM交AB于点M，交FD于点N．则∠A，∠AME，∠CEG之间存在怎样的数量关系？请写出证明过程；
（2）如图2，在（1）的条件下，若EG平分∠AED，∠AME＝35°，且∠EDF﹣∠A＝30°，求∠C的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知长方形ABCD中，∠A=∠D=∠B=∠C=90,E是AD上的一点，F是AB上的一点，EF⊥EC，且EF＝EC，DE=4cm.
(1)求证：AF=DE.
(2)若AD+DC=18，求AE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
