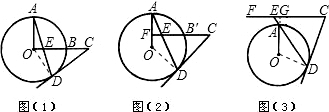
(1)证明:连接OD,
OD⊥CD,∠CDE+∠ODA=90°;
在Rt△AOE中,
∠AEO+∠A=90°;
在⊙O中,
∵OA=OD,
∴∠A=∠ODA,∠CDE=∠AEO,
又∵∠AEO=∠CED,
∴∠CED=∠CDE,CD=CE;
(2)解:CE=CD仍然成立,
∵原来的半径OB所在直线向上平行移动,
∴CF⊥AO于F;
在Rt△AFE中,
∠A+∠AEF=90°,
连接OD,则
∠ODA+∠CDE=90°,且OA=OD,
∴∠A=∠ODA,∠AEF=∠CDE;
又∵∠AEF=∠CED,
∴∠CED=∠CDE,CD=CE;
(3)解:CE=CD仍成立,
∵原来的半径OB所在直线向上平行移动,
∴AO⊥CF,
延长OA交CF于G,
在Rt△AEG中,
∠AEG+∠GAE=90°;
连接OD,有,
∠CDA+∠ODA=90°,且OA=OD,
∴∠ADO=∠OAD=∠GAE,
∴∠CDE=∠CED,
∴CD=CE.
分析:(1)可连接OD,通过等边对等角(∠OAD=∠ODA),等角的余角相等(∠OAE+∠OEA=90°,∠ODA+∠CDE=90°),
以及对顶角相等(∠AEO=∠CED),将相等的角进行置换即可得出∠CDE=∠CED,即CD=CE;
(2)连接OD方法和(1)完全相同;
(3)延长OA交CF于G,由于CF是上下平行移动,因此OG⊥CF,证法同(1).
点评:本题主要考查了切线的性质,本题中虽然CF的位置不一样但都是根据切线的性质,等边对等角,等角的余角相等来求解的.

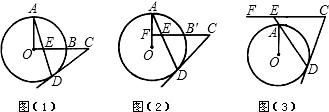
 (1)证明:连接OD,
(1)证明:连接OD,

 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=