
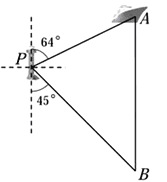
【题目】如图,一艘海轮位于灯塔![]() 的北偏东
的北偏东![]() 方向,距离灯塔120海里的
方向,距离灯塔120海里的![]() 处,它沿正南方向航行一段时间后,到达位于灯塔
处,它沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东
的南偏东![]() 方向上的
方向上的![]() 处,求
处,求![]() 和
和![]() 的长(结果取整数).
的长(结果取整数).
参考数据:![]() ,
,![]() 取
取![]() .
.
【答案】BP=153;BA=161.
【解析】
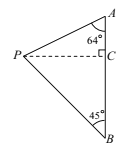
试题分析:如图,过点P作PC⊥AB,垂足为C,由题意可知,∠A=64°,∠B=45°,PA=120,在Rt△APC中,求得PC、AC的长;在Rt△BPC中,求得BP、BC的长,即可得BA的长.
试题解析:如图,过点P作PCAB,垂足为C,
由题意可知,∠A=64°,∠B=45°,PA=120,
在Rt△APC中,sin∠A=![]() ,
,
∴PC=PA·sin∠A=120×sin64°,
AC=PA×cos∠A=120×cos64°,
在Rt△BPC中,sin∠B=![]() ,
,
∴BP=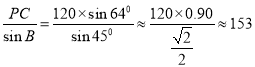
BC=![]()
∴BA=BC+AC=120×sin64°+120×cos64°≈120×0.90+120×0.44≈161.
答:BP的长约有153海里,BA的长约有161海里.


科目:初中数学 来源: 题型:
【题目】【探究函数y=x+![]() 的图象与性质】
的图象与性质】
(1)函数y=x+![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
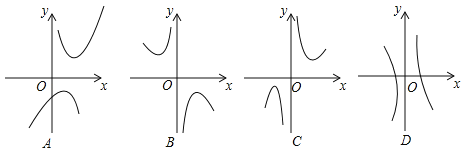
(2)下列四个函数图象中函数y=x+![]() 的图象大致是 ;
的图象大致是 ;
(3)对于函数y=x+![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下列的求解过程补充完整.
解:∵x>0
∴y=x+![]() =(
=(![]() )2+(
)2+(![]() )2=(
)2=(![]() ﹣
﹣![]() )2+
)2+
∵(![]() ﹣
﹣![]() )2≥0
)2≥0
∴y≥ .
[拓展运用]
(4)若函数y=![]() ,则y的取值范围 .
,则y的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.
(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com