
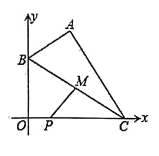
【题目】如图,已知点![]() 、
、![]() ,
,![]() 为
为![]() 轴正半轴上的一个动点,以
轴正半轴上的一个动点,以![]() 为边构造
为边构造![]() ,使点
,使点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .若
.若![]() 为
为![]() 的中点,则
的中点,则![]() 的最小值为___________.
的最小值为___________.
【答案】![]()
【解析】
先确定M点的轨迹为直线,当PM⊥M1M2时,PM最小,可以证明△PMM2∽△M1OM2,即可求解.
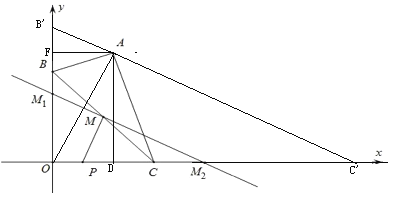
当B在原点时,作OA⊥AC交x轴于C’,作AD⊥x轴于D点
∴AD=4, OD=2
∵∠AOD+∠OAD=∠AOD+∠AC’D=90°
∴∠OAD=∠AC’D
∴tan∠OAD=tan∠AC’D
∴![]()
∴C’D=8
∴BC’=10,故点M2(5,0);
当C在原点时,作AF⊥y轴于F点
同理可得tan∠OAD=tan∠B’AF=![]()
∴BF’=![]() AF=1
AF=1
∴B’(0,5),故M1(0,![]() ),
),
∵当PM⊥M1M2时,PM最小,
∵∠MM2P=∠OM2M1,∠PMM2=∠M1OM2=90°
∴△PMM2∽△M1OM2,
∴![]() ,
,
∵M1M2=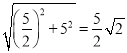 ,M1O=
,M1O=![]() , PM2=5-1=4
, PM2=5-1=4
∴PM=![]() ;
;
故答案为![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
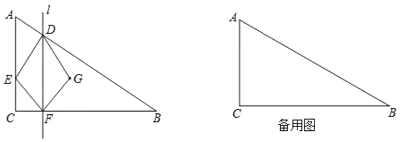
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以
出发,以![]() 的速度分别沿
的速度分别沿![]() 、
、![]() 匀速运动,当点
匀速运动,当点![]() 到达点
到达点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() .过点
.过点![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
(1)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 的平分线上;
的平分线上;
(2)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 边上;
边上;
(3)设![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写
之间的函数关系式,并写![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
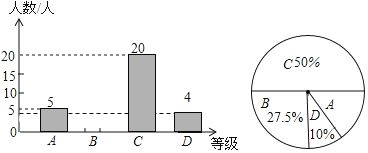
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)数学理解:如图①,![]() 是等腰直角三角形,过斜边
是等腰直角三角形,过斜边![]() 的中点
的中点![]() 作正方形
作正方形![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
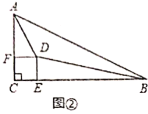
(2)问题解决:如图②,在任意直角![]() 内,找一点
内,找一点![]() ,过点
,过点![]() 作正方形
作正方形![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
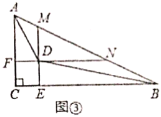
(3)联系拓广;如图③,在(2)的条件下,分别延长![]() ,
,![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
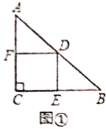
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的右侧),与
的右侧),与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 、
、![]() 、
、![]() 的坐标:
的坐标:
(2)当以![]() 为圆心的圆与
为圆心的圆与![]() 轴和直线
轴和直线![]() 都相切时,求抛物线的解析式:
都相切时,求抛物线的解析式:
(3)在(2)的条件下,如图2.![]() 是
是![]() 轴负半轴上的一点,过点
轴负半轴上的一点,过点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ,使得
,使得![]() 恰好落在
恰好落在![]() 轴上?若存在,请求出
轴上?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距![]() 车和
车和![]() 车分别从甲地和乙地同时出发,相向而行,沿同一 条公路驶往乙地和甲地
车分别从甲地和乙地同时出发,相向而行,沿同一 条公路驶往乙地和甲地![]() 后,
后,![]() 车因临时需要,返回到这条公路上的丙地取物,然后又立即赶往乙地,结果比
车因临时需要,返回到这条公路上的丙地取物,然后又立即赶往乙地,结果比![]() 车晚
车晚![]() 到达目的地.两车的速度始终保持不变,如图是
到达目的地.两车的速度始终保持不变,如图是![]() 两车距各自出 发地的路程
两车距各自出 发地的路程![]() (单位:
(单位:![]() ),
),![]() (单位:
(单位:![]() )与
)与![]() 车出发时间
车出发时间![]() (单位:
(单位:![]() )的函数图象,请结合图象信息解答下列问题:
)的函数图象,请结合图象信息解答下列问题:

(1)A车的速度为 ![]() 车的速度为
车的速度为
(2)求甲、丙两地的距离;
(3)求![]() 车出发多长时间,两车相距
车出发多长时间,两车相距![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次购进20件A商品,40件B商品,共用了1980元.脱销后,在进价不变的情况下,第二次购进40件A商品,20件B商品,共用了1560元.商品A的售价为每件30元,商品B的售价为每件60元.
(1)求A,B两种商品每件的进价分别是多少元?
(2)为了满足市场需求,需购进A,B两种商品共1000件,且A种商品的数量不少于B种商品数量的3倍,请你设计进货方案,使这1000件商品售完后,商场获利最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com